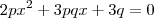 , a soma das raízes é
, a soma das raízes é 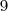 e o produto
e o produto 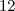 . calcule
. calcule  .
.tenso esse exercício.
Saca esse aqui,
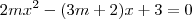 tenha raízes reais e desiguais.
tenha raízes reais e desiguais.Como assim desiguais? tenso.

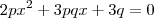 , a soma das raízes é
, a soma das raízes é 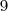 e o produto
e o produto 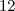 . calcule
. calcule  .
.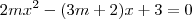 tenha raízes reais e desiguais.
tenha raízes reais e desiguais.
![\\
x_1 = \frac{-b - \sqrt[]{b^2 - 4ac}}{2a} \\
x_2 = \frac{-b + \sqrt[]{b^2 - 4ac}}{2a} \\
x_1 = \frac{-b - \sqrt[]{b^2 - 4ac}}{2a} \\
x_2 = \frac{-b + \sqrt[]{b^2 - 4ac}}{2a}](/latexrender/pictures/e9d32f2db086ebdd9c13b5ac66bb8870.png)
![\\
x_1 = \frac{-3pq - \sqrt[]{(3pq)^2 - 4*2p*3q}}{2*2p} \\
x_2 = \frac{-3pq + \sqrt[]{(3pq)^2 - 4*2p*3q}}{2*2p} \\
x_1 = \frac{-3pq - \sqrt[]{(3pq)^2 - 4*2p*3q}}{2*2p} \\
x_2 = \frac{-3pq + \sqrt[]{(3pq)^2 - 4*2p*3q}}{2*2p}](/latexrender/pictures/42813d1f7e6d82f122c252bbeaa75cbe.png)
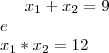
![\\
\frac{-3pq - \sqrt[]{(3pq)^2 - 4*2p*3q}}{2*2p} + \frac{-3pq + \sqrt[]{(3pq)^2 - 4*2p*3q}}{2*2p} = 9 \\
\frac{-3pq - \sqrt[]{(3pq)^2 - 4*2p*3q}}{2*2p} * \frac{-3pq + \sqrt[]{(3pq)^2 - 4*2p*3q}}{2*2p} = 12 \\
\frac{-3pq - \sqrt[]{(3pq)^2 - 4*2p*3q}}{2*2p} + \frac{-3pq + \sqrt[]{(3pq)^2 - 4*2p*3q}}{2*2p} = 9 \\
\frac{-3pq - \sqrt[]{(3pq)^2 - 4*2p*3q}}{2*2p} * \frac{-3pq + \sqrt[]{(3pq)^2 - 4*2p*3q}}{2*2p} = 12](/latexrender/pictures/81b500ad718fc51a7b7ace18b156d30a.png)
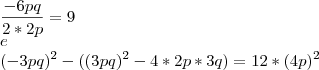


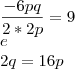


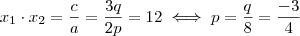

 . Basta calcular o discriminante e definir que ele seja maior ou igual a zero.
. Basta calcular o discriminante e definir que ele seja maior ou igual a zero.


Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)