Materiais sobre Álgebra.
Utilize a seção de pedidos para outros que não estejam disponíveis.
As fontes dos arquivos serão diversas e deverão ser citadas sempre que possível, mantendo totalmente os créditos dos respectivos autores.
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por futuro fisico » Sáb Jul 02, 2011 17:23
por futuro fisico » Sáb Jul 02, 2011 17:23
não sei como determinar a dimensão do espaço linear....
questão:
Determinar dimensão do espaço linear indicado: a) espaço de matrizes n × m com elementos reais (complexos)
só quero que me digam como determinar,por exemplo:
se houver formula qual....,se for por dedução como....
meu prof. explicou por cima d+
desde ja agradeço!
P.S.: não é cola, é urgente
-
futuro fisico
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Jun 25, 2011 18:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: fisica medica
- Andamento: cursando
 por Renato_RJ » Dom Jul 03, 2011 14:12
por Renato_RJ » Dom Jul 03, 2011 14:12
Que eu me lembre, a dimensão de um espaço vetorial é a quantidade de vetores que formam a sua base. Na sua questão o espaço vetorial são as matrizes nxm, logo entendo que a dimensão gerada por essas matrizes tenha dimensão nxm, como você fala que é formada por elementos reais, então
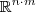
.
Abs.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por futuro fisico » Dom Jul 03, 2011 15:59
por futuro fisico » Dom Jul 03, 2011 15:59
gostaria de saber se existe uma resposta mais detalhada se eu colocar isso numa prova meu professor me da 0 na questão
no aguardo!
-
futuro fisico
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Jun 25, 2011 18:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: fisica medica
- Andamento: cursando
 por Renato_RJ » Dom Jul 03, 2011 17:13
por Renato_RJ » Dom Jul 03, 2011 17:13
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
Voltar para Álgebra
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- algebra linear - base e dimensão do espaço de funçoes
por mou_duarte » Seg Mai 02, 2016 11:14
- 0 Respostas
- 1979 Exibições
- Última mensagem por mou_duarte

Seg Mai 02, 2016 11:14
Álgebra Linear
-
- [Espaço Vetorial] Dimensão
por joao_al_campos » Sáb Abr 07, 2012 13:27
- 5 Respostas
- 3107 Exibições
- Última mensagem por LuizAquino

Seg Abr 09, 2012 16:14
Álgebra Linear
-
- [Álgebra Linear]-Base e dimensão
por Ana_Rodrigues » Seg Mai 07, 2012 18:36
- 2 Respostas
- 3016 Exibições
- Última mensagem por Ana_Rodrigues

Ter Mai 08, 2012 23:12
Álgebra Linear
-
- [Álgebra Linear] Ache a dimensão do subespaço...
por gabriel17carmo » Sex Jun 08, 2012 23:16
- 5 Respostas
- 3873 Exibições
- Última mensagem por gabriel17carmo

Seg Jun 11, 2012 02:42
Álgebra Linear
-
- ESPAÇO LINEAR
por p1a2u3lo » Dom Set 18, 2016 11:01
- 0 Respostas
- 1380 Exibições
- Última mensagem por p1a2u3lo

Dom Set 18, 2016 11:01
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


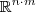 .
.
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
