(ufmt) o lado, o semiperimetro e a área de um hexágono regular formam,nessa ordem,uma PG. Determine o apótema desse hexágono.
me ajudem...
se conseguirem fazer me digam com chegaram ao resultado..
obrigado



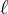 tem semiperímetro dado por
tem semiperímetro dado por 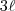 e área dada por
e área dada por 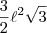
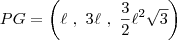
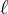 . Para isso use a fórmula de PG, onde diz que o segundo termo dividido pelo segundo termo é igual ao segundo termo dividido pelo primeiro termo. Assim você vai descobrir o valor de
. Para isso use a fórmula de PG, onde diz que o segundo termo dividido pelo segundo termo é igual ao segundo termo dividido pelo primeiro termo. Assim você vai descobrir o valor de 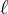 .
.

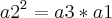
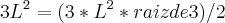
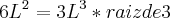
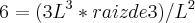
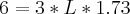
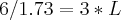
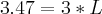
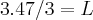
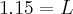

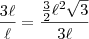
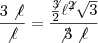
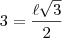
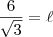
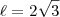
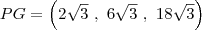 de razão 3.
de razão 3.



Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes