Determinar o angulo entre as seguintes retas:
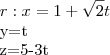

Minha dúvida é: Qual seria o vetor "s" ?
Joguei na fórmula os valores:
r=(1,1,-3) e em, s=(0,0,1) e o resultado q obtive não é o que consta na resolução.

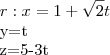






 .
.
Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: