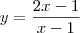Considere a seguinte fórmula para x?? : f (x)=x?1
x?2 .
a) Qual é o Dom( f ) , ou seja, o domínio de f(x), e qual é a Im(f ) , ou seja
a imagem de f(x)?
b) Mostre que a função f é inversível no seu domínio e calcule a função
inversa. Qual é o domínio da função inversa?
a)Seria o dominio N ou seja todos os numeros naturais? e a imagem Z maiores ou igqual a -1?
b)x=y-1 essa seria sua inversa?Se puderem me esclarecer....


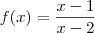 ou
ou 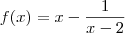 ? Por favor, procure usar latex nas suas próximas postagens.
? Por favor, procure usar latex nas suas próximas postagens.


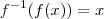
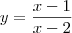 substituindo y por x reciprocamente e resolvendo em ordem a y, obtem-se:
substituindo y por x reciprocamente e resolvendo em ordem a y, obtem-se: