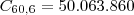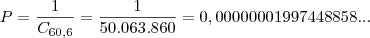Há algum tempo o site da Caixa Econômica Federal informava "fórmulas" para os cálculos das probabilidades.
Considerando algumas buscas de visitantes por este assunto aqui na Ajuda Matemática e o fato de que atualmente a Caixa apenas informa a probabilidade, sem mais detalhes sobre o cálculo (http://www.caixa.gov.br/loterias/loterias/megasena/probabilidades.asp), eis um comentário para obtermos a probabilidade de acerto informada para 6 dezenas que é de 1 em 50.063.860 (50 milhões 63 mil 860).
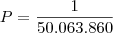
Veja este número em representação decimal:
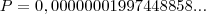
E o percentual de acerto:
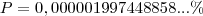
São 6 dezenas sorteadas dentre 60, sem repetição:

Vamos entender o processo.
No sorteio da primeira dezena, temos todas as 60 dezenas disponíveis, ou seja, temos 60 possibilidades:
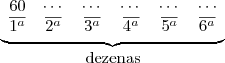
No sorteio da segunda, como não há repetição da dezena, restam 59 possibilidades:

Até que no sorteio da última dezena, serão 55 possibilidades:

Pelo
Princípio Fundamental da Contagem: Se há 60 maneiras para 1ª dezena ser sorteada
E 59 maneiras para a 2ª dezena ser sorteada ...
E 55 maneiras para a 6ª dezena ser sorteada, o número total de maneiras para o sorteio ocorrer será o
produto destas possibilidades, ou seja:

(36 bilhões 45 milhões 979 mil e 200 possibilidades)
Dicas para outras pesquisas: rule of product / basic counting principle / the fundamental principle of counting
Em cada conjunto de 6 dezenas, pode haver
permutação e ainda assim será considerado o mesmo sorteio.
Da
combinatória, se temos

elementos distintos, podemos obter
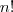
arranjos destes elementos.
Estes arranjos são chamados de
permutações.
De modo que o número total possível de jogos será, de fato, menor.
Porque até então, temos
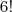
"jogos repetidos" neste número "

".
Então, para encontrarmos o número total de jogos sem estas repetições, devemos dividir por
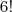
.
total possível de sorteios na Mega Sena =

Na prática, pela teoria combinatória, este é o
número de combinações de n elementos distintos tomados de p em p.
Pode ser obtido diretamente por esta "fórmula" (cuja origem é análoga a este processo acima):

Veja como obtemos o mesmo resultado:

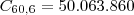
Como a probabilidade é o quociente entre a quantidade de eventos favoráveis, sobre a quantidade de eventos possíveis, então finalmente podemos representar a probabilidade de acerto na Mega Sena:
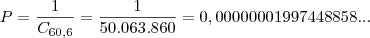



![[0, 1] [0, 1]](/latexrender/pictures/264884439b70ab09a86bc848421c6de6.png) .
. .
.
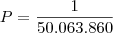
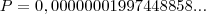
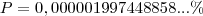

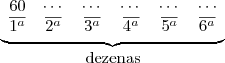


 (36 bilhões 45 milhões 979 mil e 200 possibilidades)
(36 bilhões 45 milhões 979 mil e 200 possibilidades) elementos distintos, podemos obter
elementos distintos, podemos obter 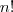 arranjos destes elementos.
arranjos destes elementos.



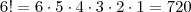
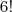 "jogos repetidos" neste número "
"jogos repetidos" neste número " ".
".