 por hopiloto » Seg Jun 20, 2011 23:21
por hopiloto » Seg Jun 20, 2011 23:21
QUERO SABER COMO RESOLVER :
ENCONTRE A FORMULA PARA Sn EM TERMOS DE n E TAMBEM SE ELA É DIVERGENTE OU NÃO : An = 2n+1/3n+2
-
hopiloto
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sex Dez 10, 2010 00:13
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia ambiental
- Andamento: cursando
 por nietzsche » Sex Jun 24, 2011 14:14
por nietzsche » Sex Jun 24, 2011 14:14
olá hopiloto,
sobre a convergência: a série
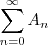
é divergente, pois uma condição necessária para que ela convirja é
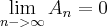
, que não é satisfeita:
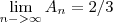
.
abraço
-
nietzsche
- Usuário Parceiro

-
- Mensagens: 99
- Registrado em: Qua Jan 12, 2011 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por hopiloto » Qui Jun 30, 2011 00:21
por hopiloto » Qui Jun 30, 2011 00:21
nietzsche escreveu:olá hopiloto,
sobre a convergência: a série
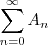
é divergente, pois uma condição necessária para que ela convirja é
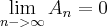
, que não é satisfeita:
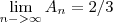
.
abraço
Ola, disso eu sabia

So não estava conseguindo entender como resolver, porque o enuciado da questão diz: ESCREVA OS QUATRO PRIMEIROS TERMOS E DETERMINE SE ELA É CONVERGENTE OU DIVERGENTE [b]E SE CONVERGE, OBTENHA A SUA SOMA.
Mas nesse caso entendi você usou o teste da divergência (TD). Mas quando o limite der zero = COMVERGENTE, como vou encontrar a soma (Sn)?????
-
hopiloto
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sex Dez 10, 2010 00:13
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia ambiental
- Andamento: cursando
 por MarceloFantini » Qui Jun 30, 2011 08:04
por MarceloFantini » Qui Jun 30, 2011 08:04
Tome cuidado! Limite do termo geral ir pra zero não é garantia de convergência, veja a série harmônica
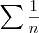
. Hopiloto, por favor da próxima vez coloque o enunciado da questão inteira, ficaria mais fácil de saber o que era pedido.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por nietzsche » Sex Jul 08, 2011 19:03
por nietzsche » Sex Jul 08, 2011 19:03
a soma vc pode obter calculando os termos de Sn para n = 1, depois, n=2, n=3, e assim por diante. Vc vai ter que conseguir perceber algum padrão nessas somas parciais.
por exemplo,
An = 2n+1/3n+2
se n=1:
S1 = A1 = 2(1) + 1/3(1)+2
se n=2:
S2 = A1 + A2 = A1 + 2(2) + 1/3(2) +2
se n=3
S3 = A1 + A2 + A3
se n=k
Sn = A1 + A2 + A3 + ... + Ak-1 + Ak
É meio chatinho de achar o Sn por causa das contas.
-
nietzsche
- Usuário Parceiro

-
- Mensagens: 99
- Registrado em: Qua Jan 12, 2011 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Aparecida » Qua Fev 01, 2012 22:09
por Aparecida » Qua Fev 01, 2012 22:09
BOA NOITE, FAZ\ UM TEMPINHO QUE NAO VEJO O CONTEUDO SOBRE SEQUENCIA E ESTOU COM DUVIDAS, SOBRE O QUE É SEQUENCIA i-agonais. queria saber a formula.
Uma explicação.
-
Aparecida
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Dom Out 30, 2011 22:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: formado
Voltar para Sequências
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



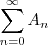 é divergente, pois uma condição necessária para que ela convirja é
é divergente, pois uma condição necessária para que ela convirja é 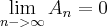 , que não é satisfeita:
, que não é satisfeita: 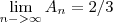 .
.
é divergente, pois uma condição necessária para que ela convirja é
, que não é satisfeita:
.

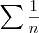 . Hopiloto, por favor da próxima vez coloque o enunciado da questão inteira, ficaria mais fácil de saber o que era pedido.
. Hopiloto, por favor da próxima vez coloque o enunciado da questão inteira, ficaria mais fácil de saber o que era pedido.




 .
.



