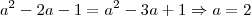Olá pessoal, poderiam me ajudar na questão a seguir:
Dados os vetores u=(1, a, -2a-1), v=(a,a-1,1) e w=(a,-1,1), determinar "a" de modo que u.v=(u+v)w.
Cheguei a conclusão que a=2 fazendo o seguinte:
u.v=(1,a,-2a-1)(a,a-1,1)=a²-2a-1
u+v=(1+a,2a-1,-2a)
(u+v)w=a²-3a+1
u.v=(u+v)w
a²-2a-1=a²-3a+1
a=2