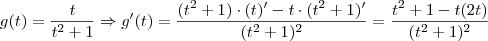por valeuleo » Ter Jun 21, 2011 21:50
por valeuleo » Ter Jun 21, 2011 21:50
Não estou conseguindo resolver essa daqui:

Calculei a derivada e obtive:

. Daqui em diante não consegui resolver. Podem me ajudar?
Grato
-
valeuleo
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Qua Mar 23, 2011 14:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências da Computação
- Andamento: cursando
 por valeuleo » Ter Jun 21, 2011 22:29
por valeuleo » Ter Jun 21, 2011 22:29
MarceloFantini escreveu:Tome cuidado, você errou ao derivar a função:
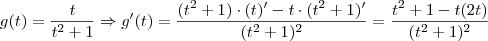

Onde esta função for positiva, a função original é crescente, onde ela for zero é um possível máximo ou mínimo, e onde for negativa ela será decrescente. Pense na interpretação geométrica disso: uma derivada representa o coeficiente angular da reta tangente naquele ponto. Positivo indica reta "para cima", crescendo, e negativo indica "para baixo", decrescendo.
Valeu. Realmente não tinha notado no errinho na derivação. Grato
-
valeuleo
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Qua Mar 23, 2011 14:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências da Computação
- Andamento: cursando
 por LuizAquino » Ter Jun 21, 2011 22:44
por LuizAquino » Ter Jun 21, 2011 22:44
Se você não souber como continuar o exercício, eu recomendo que assista a
vídeo-aula "20. Cálculo I - Crescimento, Decrescimento e Concavidade do Gráfico de Funções".
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calcular intervalos de crescimento e decrescimento da função
por Eduardooitavo » Sáb Jun 09, 2012 18:06
- 1 Respostas
- 2520 Exibições
- Última mensagem por MarceloFantini

Sáb Jun 09, 2012 19:32
Cálculo: Limites, Derivadas e Integrais
-
- crescimento e decrescimento da função
por Ana Maria da Silva » Qua Out 02, 2013 10:18
- 1 Respostas
- 1155 Exibições
- Última mensagem por Bravim

Qui Out 03, 2013 05:32
Cálculo: Limites, Derivadas e Integrais
-
- crescimento e decrescimento
por joandro » Dom Abr 13, 2014 11:30
- 1 Respostas
- 1459 Exibições
- Última mensagem por alienante

Ter Abr 29, 2014 17:27
Cálculo: Limites, Derivadas e Integrais
-
- Intervalo de crescimento e decrescimento
por valeuleo » Qui Jun 23, 2011 12:02
- 4 Respostas
- 2833 Exibições
- Última mensagem por LuizAquino

Sáb Jun 25, 2011 16:50
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] crescimento e decrescimento
por fabriel » Ter Set 25, 2012 02:57
- 2 Respostas
- 1919 Exibições
- Última mensagem por fabriel

Ter Set 25, 2012 12:57
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

 . Daqui em diante não consegui resolver. Podem me ajudar?
. Daqui em diante não consegui resolver. Podem me ajudar?

 . Daqui em diante não consegui resolver. Podem me ajudar?
. Daqui em diante não consegui resolver. Podem me ajudar?