 por felipealves » Ter Jun 21, 2011 11:48
por felipealves » Ter Jun 21, 2011 11:48
Olá a todos, estou com uma grande dúvida, na integração de questões com sen(2x),cos(3X),entre outras, a duvida é que quando faço a integral, no resultado há uma fração mas não consigo encontrar de onde vem essa fração, por fovor me tirem essa dúvida.
-
felipealves
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Jun 21, 2011 11:33
- Localização: Natal, RN
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Ciências e Tecnologia
- Andamento: cursando
 por Fabio Cabral » Ter Jun 21, 2011 13:12
por Fabio Cabral » Ter Jun 21, 2011 13:12
Veja:

Quem você precisa derivar para obter

? Seria
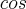
, não é verdade?

Porém, se você derivar
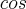
, terá como resultado
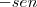
, Logo, você precisaria derivar

para obter

.

Sabendo disso, tente derivar

.
Aplicando a regra da cadeia temos:
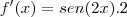
, correto?
Porém, o que você quer é

(veja na sua integral). Então, teremos que pensar numa maneira de tirar esse

daí. Como? Dividindo por 2.
Veja:

=

Ou:
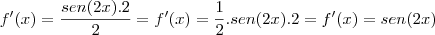
- Conserve a primeira e multiplique pelo inverso da segunda.
Logo,
Sua integral é:

Ps.: Escrevi bem depressa. mas creio que esteja tudo certo. Caso contrário, peço que informe o erro.
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por LuizAquino » Ter Jun 21, 2011 16:30
por LuizAquino » Ter Jun 21, 2011 16:30
Deseja-se resolver integrais do tipo

, com
k uma constante não nula.
Fazendo a substituição

, temos que

(ou seja,

).
Desse modo, a integral será equivalente a

. Resolvendo essa integral, obtemos
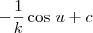
, com
c uma constante real.
Portanto, temos que
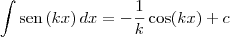
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por felipealves » Ter Jun 21, 2011 20:59
por felipealves » Ter Jun 21, 2011 20:59
Valeu pessoal,obrigado por tirarem a minha dúvida. Conseguir ver onde eu estava errando, agora ficou mais fácil.
-
felipealves
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Jun 21, 2011 11:33
- Localização: Natal, RN
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Ciências e Tecnologia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral indefinida
por gdarius » Ter Mar 16, 2010 15:57
- 5 Respostas
- 5622 Exibições
- Última mensagem por DanielFerreira

Sáb Mar 31, 2012 19:32
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinida
 por CrazzyVi » Ter Ago 17, 2010 21:41
por CrazzyVi » Ter Ago 17, 2010 21:41
- 1 Respostas
- 2704 Exibições
- Última mensagem por Lucio Carvalho

Qua Ago 18, 2010 08:27
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] indefinida
por Aliocha Karamazov » Qui Mar 01, 2012 20:30
- 7 Respostas
- 5041 Exibições
- Última mensagem por Aliocha Karamazov

Sáb Mar 03, 2012 21:59
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinida - 2
por DanielFerreira » Sáb Mar 31, 2012 18:31
- 1 Respostas
- 2062 Exibições
- Última mensagem por LuizAquino

Sáb Mar 31, 2012 18:53
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinida - 3
por DanielFerreira » Sáb Mar 31, 2012 18:41
- 2 Respostas
- 2093 Exibições
- Última mensagem por DanielFerreira

Sáb Mar 31, 2012 19:20
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 ? Seria
? Seria 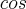 , não é verdade?
, não é verdade? 
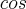 , terá como resultado
, terá como resultado 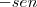 , Logo, você precisaria derivar
, Logo, você precisaria derivar  para obter
para obter  .
. 
 .
.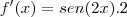 , correto?
, correto? (veja na sua integral). Então, teremos que pensar numa maneira de tirar esse
(veja na sua integral). Então, teremos que pensar numa maneira de tirar esse  daí. Como? Dividindo por 2.
daí. Como? Dividindo por 2. =
= 
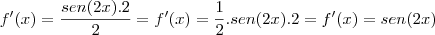


 , com k uma constante não nula.
, com k uma constante não nula. , temos que
, temos que  (ou seja,
(ou seja,  ).
). . Resolvendo essa integral, obtemos
. Resolvendo essa integral, obtemos 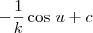 , com c uma constante real.
, com c uma constante real.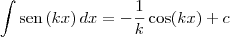 .
.






