 por Civil UFSCar » Seg Jun 20, 2011 16:04
por Civil UFSCar » Seg Jun 20, 2011 16:04
Pessoal, não consigo fazer essa integral:
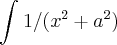
não é que eu não tenha tentado, eu simplesmente não sei!
que tipo ela é? que passos ou processos vocês utilizariam? obrigado pela ajuda.
-
Civil UFSCar
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Jun 20, 2011 15:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia civil
- Andamento: cursando
 por FilipeCaceres » Seg Jun 20, 2011 16:56
por FilipeCaceres » Seg Jun 20, 2011 16:56
Pode ser que alguém tenha uma dica melhor,mas vê se você consegue resolver com esta observação.

Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por LuizAquino » Seg Jun 20, 2011 19:48
por LuizAquino » Seg Jun 20, 2011 19:48
Note que
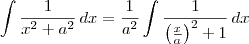
.
Faça a substituição
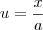
e lembre-se da dica dada por
FilipeCaceres.
Vale lembrar que

é o arco-tangente de x, também denotado por
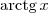
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Civil UFSCar » Seg Jun 20, 2011 20:05
por Civil UFSCar » Seg Jun 20, 2011 20:05
É eu acho que eu entendi agora gente.... Não sabia que o "a" era constante
VALEEEUU
-
Civil UFSCar
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Jun 20, 2011 15:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia civil
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Estou com dificuldade para resolver esta integral
por Paulo Perez » Qui Out 03, 2013 12:22
- 2 Respostas
- 4612 Exibições
- Última mensagem por Paulo Perez

Sex Out 04, 2013 16:32
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] Integral por partes! Alguem pode me ajudar?
por mih123 » Qua Jan 16, 2013 20:18
- 3 Respostas
- 4581 Exibições
- Última mensagem por adauto martins

Qua Out 22, 2014 09:11
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Resolver Integral definida com trigonometria
por rodrigoboreli » Dom Set 07, 2014 01:02
- 1 Respostas
- 4344 Exibições
- Última mensagem por adauto martins

Sex Out 17, 2014 12:39
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Qua Ago 17, 2011 22:33
- 2 Respostas
- 2843 Exibições
- Última mensagem por ewald

Qui Ago 18, 2011 00:54
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Sáb Ago 20, 2011 17:20
- 2 Respostas
- 2867 Exibições
- Última mensagem por LuizAquino

Dom Ago 21, 2011 21:14
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
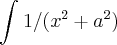

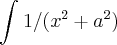



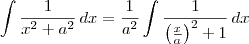 .
.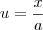 e lembre-se da dica dada por FilipeCaceres.
e lembre-se da dica dada por FilipeCaceres. é o arco-tangente de x, também denotado por
é o arco-tangente de x, também denotado por 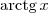 .
.

