 por Maykids » Seg Jun 20, 2011 02:27
por Maykids » Seg Jun 20, 2011 02:27
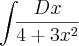
vai dar isso:
![\frac{\sqrt[]{3}}{6}arctg + \frac{\sqrt[]{3}x}{2} + C \frac{\sqrt[]{3}}{6}arctg + \frac{\sqrt[]{3}x}{2} + C](/latexrender/pictures/391bcea0c5f058296a4e146339c92a06.png)
o que eu quero saber é como que eu vo de uma integral como que eu acho que ela vai dar arctg, se tem propriedades que me diz isso..
desde ja agradeço...
-
Maykids
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Dom Mar 20, 2011 12:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de computação
- Andamento: cursando
 por Maykids » Seg Jun 20, 2011 14:23
por Maykids » Seg Jun 20, 2011 14:23
eu pesei em algo com 1/ x^2+1 so que mesmo assim tem o 4 e o 3 que multiplica x^2 então eu nao tenho noção de como se chegar até ali..
-
Maykids
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Dom Mar 20, 2011 12:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de computação
- Andamento: cursando
 por carlosalesouza » Seg Jun 20, 2011 17:52
por carlosalesouza » Seg Jun 20, 2011 17:52
Integral não é exatamente algo simples... não é fim do mundo, mas possui muitas propriedades envolvidas... as chamadas tecnicas de integração...
Nesse caso, essa função deve ser integrada por substituição trigonométrica, utilizando identidades e relações trigonométricas, para chegar a uma função integrável, que resultará nessa função que está expressa...
Não vai adiantar muito eu ou outra pessoa simplesmente resolver a integral, pois só vai te servir se vc pegar outra função muito similar para integrar... eu recomendo que vc procure um livro de cálculo ou mesmo uma pesquisada na net... sobre tecnicas de integraçõ... estude cada uma delas... por substituição, por partes, por potencias trigonometricas, por substituição trigonometrica, enfim... daí vc vai conseguir embasamento...
É claro que vc pode sempre retornar com as dúvidas que resultarem desse estudo...
boa sorte e um grande abraço...
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
 por Maykids » Seg Jun 20, 2011 18:52
por Maykids » Seg Jun 20, 2011 18:52
Eu nao tenho ela resolvida nao, rs apenas as resposta ...foi uma lista que ele criou, vou dar uma estudada nessas tecnicas e hoje mesmo ja posto alguma coisa,
obrigado ai por tudo.
att,
Maycon Carlete
-
Maykids
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Dom Mar 20, 2011 12:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de computação
- Andamento: cursando
 por LuizAquino » Seg Jun 20, 2011 20:04
por LuizAquino » Seg Jun 20, 2011 20:04
Veja as dicas dadas no tópico:
Integral!viewtopic.php?f=120&t=5176
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Exponencial de número complexo. Como saio dessa?
por andrina » Sex Nov 19, 2010 15:16
- 1 Respostas
- 2224 Exibições
- Última mensagem por luispereira

Sex Dez 24, 2010 13:24
Números Complexos
-
- como resolver a integral de y² . e^y²
por Anniinha » Ter Ago 16, 2011 18:57
- 10 Respostas
- 6123 Exibições
- Última mensagem por LuizAquino

Qua Ago 17, 2011 17:25
Cálculo: Limites, Derivadas e Integrais
-
- Integral, como resolver??
por manuoliveira » Qua Out 17, 2012 21:40
- 2 Respostas
- 1909 Exibições
- Última mensagem por e8group

Qui Out 18, 2012 11:10
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] como calcular
por ghiza » Seg Jul 15, 2013 11:23
- 2 Respostas
- 1785 Exibições
- Última mensagem por ghiza

Seg Jul 15, 2013 13:24
Cálculo: Limites, Derivadas e Integrais
-
- Duvida de como resolver integral
por Manoella » Qui Fev 24, 2011 22:51
- 1 Respostas
- 1843 Exibições
- Última mensagem por LuizAquino

Dom Fev 27, 2011 19:23
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
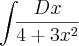
![\frac{\sqrt[]{3}}{6}arctg + \frac{\sqrt[]{3}x}{2} + C \frac{\sqrt[]{3}}{6}arctg + \frac{\sqrt[]{3}x}{2} + C](/latexrender/pictures/391bcea0c5f058296a4e146339c92a06.png)

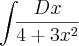
![\frac{\sqrt[]{3}}{6}arctg + \frac{\sqrt[]{3}x}{2} + C \frac{\sqrt[]{3}}{6}arctg + \frac{\sqrt[]{3}x}{2} + C](/latexrender/pictures/391bcea0c5f058296a4e146339c92a06.png)




