 por maykonnunes » Sex Jun 17, 2011 23:44
por maykonnunes » Sex Jun 17, 2011 23:44
Dado um quadrado de lado x, com centro em cada um dos vértices, traçam-se 4 circunferência de raio x. Determine a área do quatrilátero curvilíneo interior ao quadrado.
-
maykonnunes
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qua Abr 27, 2011 02:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
 por vanessafey » Sex Jun 24, 2011 13:36
por vanessafey » Sex Jun 24, 2011 13:36
Não consigo desenvolver... Acredito que seja uma figura do tipo:
Sendo assim, todas as circunferências tem um quarto de sua parte dentro do quadrado, ou seja (?r^2)/4.
Para calcular o setor que falta faremos a área do quadrado menos o que já temos A_(Q=) x^2-(?r^2)/4
A partir daí não sei mais como continuar...
-
vanessafey
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Jun 24, 2011 13:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por FilipeCaceres » Sex Jun 24, 2011 15:23
por FilipeCaceres » Sex Jun 24, 2011 15:23
Acho que você desenhou errado, acredito que o desenho correto seja este

- quadrado.png (15.12 KiB) Exibido 3538 vezes
E o que se pede é a área em verde.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por maykonnunes » Sex Jun 24, 2011 15:27
por maykonnunes » Sex Jun 24, 2011 15:27
sim felipe está certo seu desenho
-
maykonnunes
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qua Abr 27, 2011 02:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
 por vanessafey » Sex Jun 24, 2011 15:34
por vanessafey » Sex Jun 24, 2011 15:34
Então podemos traçar um triângulo eqüilátero através da intersecção entre as circunferências e os vértices do quadrado.
Por se tratar de um triângulo eqüilátero, sabemos que o mesmo também é eqüiângulo, logo, seus ângulos internos são de 60°.
Calculando a área circular deste triângulo temos que,
(60?x^2)/360?(?x^2)/6
Seria assim?? E agora? Como continuo?
- Anexos
-

-
vanessafey
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Jun 24, 2011 13:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por FilipeCaceres » Sex Jun 24, 2011 19:26
por FilipeCaceres » Sex Jun 24, 2011 19:26

- quadrado_setor.png (17.59 KiB) Exibido 3514 vezes
A área procurada é igual à área de um quadrado de lado b mais 4 vezes a área do segmento circular sombreado em verde.
1) Calcular o lado do quadrado
Seja

logo,
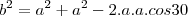
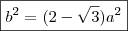
2) Calcular a área do seguimento circular
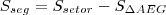
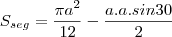

3)Área desejada
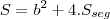


PS.: Eu calculei com o lado do quadrado ABCD valendo "a" pois não consegui definir como x no geogebra.

Fazendo a=x, temos a resposta:
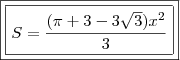
Espero que seja isso.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por vanessafey » Sáb Jun 25, 2011 16:39
por vanessafey » Sáb Jun 25, 2011 16:39
Sim, é exatamente isso.
Agora te pergunto: No geogebra conseguimos observar que alfa é 30º, mas teoricamente, não sei como provar isso...
-
vanessafey
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Jun 24, 2011 13:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por FilipeCaceres » Sáb Jun 25, 2011 17:02
por FilipeCaceres » Sáb Jun 25, 2011 17:02
Como temos uma quadrado os pontos E e G dividem o o arco BD em 3 partes iguais, sendo assim o ângulo de cada arco terá um valor igual a 30.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Trinomio Quadrado Perfeito (Complemento de quadrado)
por IgorFilipe » Qua Ago 17, 2011 23:01
- 2 Respostas
- 3753 Exibições
- Última mensagem por IgorFilipe

Qui Ago 18, 2011 15:52
Funções
-
- Quadrado
por Diocos » Qua Fev 23, 2011 18:32
- 6 Respostas
- 4475 Exibições
- Última mensagem por LuizAquino

Qui Fev 24, 2011 09:40
Geometria Plana
-
- Triangulo e Quadrado
por ginrj » Ter Mai 26, 2009 18:29
- 2 Respostas
- 2424 Exibições
- Última mensagem por ginrj

Ter Mai 26, 2009 20:26
Geometria Plana
-
- quadrado inscrito
 por mhsr » Sex Jan 15, 2010 16:03
por mhsr » Sex Jan 15, 2010 16:03
- 2 Respostas
- 2450 Exibições
- Última mensagem por mhsr

Sex Jan 15, 2010 18:12
Geometria Plana
-
- Exerc. Qui-Quadrado
por yonara » Sáb Ago 07, 2010 04:49
- 0 Respostas
- 1989 Exibições
- Última mensagem por yonara

Sáb Ago 07, 2010 04:49
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.







 logo,
logo,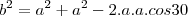
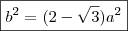
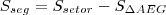
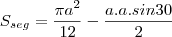

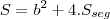



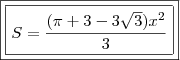





 , avisa que eu resolvo.
, avisa que eu resolvo.

