A minha ideia era encontrar a base da pirâmide, encontrar a altura (encontrando o plano em que a base está contida, e usando a fórmula de distância entre o plano e o ponto que é vértice da pirâmide) e depois colocar esses valores na fórmula para calcular o volume da pirâmide.
Primeiramente, eu calculei todas as distâncias entre esses pontos. Eu encontrei que
 ,
, 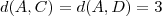 e
e  . Depois eu coloquei as coordenadas de todos os pontos e percebi que só daria certo se eu considerasse como base os segmentos BC, BD, AC e AD. Mas a figura formada por esses segmentos não forma um retângulo, mas um polígono meio estranho. Está certo o meu raciocínio? Existe outra forma melhor de encontrar o volume dessa pirâmide?
. Depois eu coloquei as coordenadas de todos os pontos e percebi que só daria certo se eu considerasse como base os segmentos BC, BD, AC e AD. Mas a figura formada por esses segmentos não forma um retângulo, mas um polígono meio estranho. Está certo o meu raciocínio? Existe outra forma melhor de encontrar o volume dessa pirâmide?

