Estava tentando resolver esta questão:
Cobrando um tiro de meta, o goleiro chuta a bola para frente e para cima, de modo que ela descreve a trajetória dada pela equação
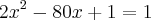
Considerando que a bola não será interceptada, é CORRETO afirmar que:
A resposta é: No ponto mais alto de sua trajetória, a bola estará a 10 metros do chão.
Primeiro, a equação não deveria ter o "a" negativo, já que a curva seria para baixo.
Segundo, achei as raízes 0 e 40. Como é uma parábola, x = 20 seria exatamente a metade (onde seria o local mais alto).
Terceiro, substituindo x por 20, dá -400...
Não compreendi.
Obrigado



