 por carlosmagnodg » Qua Jun 15, 2011 15:53
por carlosmagnodg » Qua Jun 15, 2011 15:53
Prezado Uarl, Nota-se que a questão trata-se da abordagem de Sistemas de Amortização e Juros Compostos, específicamente sistema de Amortização Francês ou mais conhecido como Sistema Price:
1º Etapa - Separando as informações:
PV - 75.000,00 i - 1% am. Período - 15 Meses - primeiramente encontrar a prestação
Calculando Com Fórmula: PMT= PV.{(i[(1+i)^n]/[(1+i)^n]-1)}
PMT = 75000 . 0,01[(1,01)^15] / [(1,01)^15)] -1
PMT = 75000. (0,011609690 / 0,160968955)
PMT = 5.409,28
Calculando com HP12C
75000 CHS, PV
1 i
15 n
PMT = ? 5.409,28
Após encontrar a prestação aplique a taxa de juros sobre o saldo devedor do período e assim fazendo período a período se você não tiver uma Calc. financeira, use o excel.
Exemplo excel:
juros = 75000*1% = 750,00 ora se os juros sobre saldo devedor do primeiro período é de $ 750 então a amortização é de (PMT 5409,28 - JUROS 750) = 4.659,28 e a partir daí você extrai o saldo devedor para próximo período que é de $ 75.000,00 - $ 4.659,28 (Amortização) = $ 70.340,72 e assim você monta a tabela Price, para encontrar o saldo devedor do Mês 09 que é de 31.349,38.
Esse valor passa a ser seu PV na nova negociação com o banco, como é informado há mudanças somente no n° de períodos e no valor presente que achamos através da tabela price, ai é só calcular novamente a prestação como abordado acima.
Calculo na HP12C
31349,38 CHS, PV
1 i
12 N
PMT = 2.785,35
Pelas minhas contas deu $ 2.785,35 - calculei no excel na calculadora e na fórmula, pode ser que a resposta disponibilizada não esteja correta ou enunciado faltando alguma informação, ou ainda, eu não tenha conseguido interpretar de forma correta a questão.
Porém, espero que tenha contribuido de alguma forma.
Bons estudos.
Seguem os cálculos no excel.
Per. Inv. Inicial PMT I Nper Amor Juros Saldo Devedor
1 -75.000,00 5.409,28 1,00% 15 4.659,28 -750,00 -70.340,72
2 -75.000,00 5.409,28 1,00% 15 4.705,88 -703,41 -65.634,84
3 -75.000,00 5.409,28 1,00% 15 4.752,94 -656,35 -60.881,91
4 -75.000,00 5.409,28 1,00% 15 4.800,46 -608,82 -56.081,44
5 -75.000,00 5.409,28 1,00% 15 4.848,47 -560,81 -51.232,97
6 -75.000,00 5.409,28 1,00% 15 4.896,95 -512,33 -46.336,02
7 -75.000,00 5.409,28 1,00% 15 4.945,92 -463,36 -41.390,09
8 -75.000,00 5.409,28 1,00% 15 4.995,38 -413,90 -36.394,71
9 -75.000,00 5.409,28 1,00% 15 5.045,34 -363,95 -31.349,38
10 -75.000,00 5.409,28 1,00% 15 5.095,79 -313,49 -26.253,59
11 -75.000,00 5.409,28 1,00% 15 5.146,75 -262,54 -21.106,84
12 -75.000,00 5.409,28 1,00% 15 5.198,22 -211,07 -15.908,62
13 -75.000,00 5.409,28 1,00% 15 5.250,20 -159,09 -10.658,43
14 -75.000,00 5.409,28 1,00% 15 5.302,70 -106,58 -5.355,73
15 -75.000,00 5.409,28 1,00% 15 5.355,73 -53,56 0,00
Per. Inv. Inicial PMT I Nper Amor Juros Saldo Devedor
1 -31.349,38 2.785,35 1,00% 12 2.471,86 -313,49 -28.877,52
2 -31.349,38 2.785,35 1,00% 12 2.496,58 -288,78 -26.380,94
3 -31.349,38 2.785,35 1,00% 12 2.521,55 -263,81 -23.859,40
4 -31.349,38 2.785,35 1,00% 12 2.546,76 -238,59 -21.312,63
5 -31.349,38 2.785,35 1,00% 12 2.572,23 -213,13 -18.740,41
6 -31.349,38 2.785,35 1,00% 12 2.597,95 -187,40 -16.142,46
7 -31.349,38 2.785,35 1,00% 12 2.623,93 -161,42 -13.518,53
8 -31.349,38 2.785,35 1,00% 12 2.650,17 -135,19 -10.868,36
9 -31.349,38 2.785,35 1,00% 12 2.676,67 -108,68 -8.191,69
10 -31.349,38 2.785,35 1,00% 12 2.703,44 -81,92 -5.488,25
11 -31.349,38 2.785,35 1,00% 12 2.730,47 -54,88 -2.757,78
12 -31.349,38 2.785,35 1,00% 12 2.757,78 -27,58 0,00
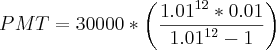


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
