





 , ou seja, temos 27 funções.
, ou seja, temos 27 funções.


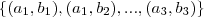

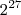 relações.
relações. ,
, ,
, , ...,
, ...,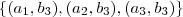 são funções em A×B.
são funções em A×B. é injetora quando
é injetora quando 
 é sobrejetora quando
é sobrejetora quando 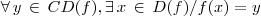
 é sobrejetora quando f é injetora e sobrejora ao mesmo tempo.
é sobrejetora quando f é injetora e sobrejora ao mesmo tempo.



FilipeCaceres escreveu:Dado os conjuntos A ={a1, a2, a3} e B ={b1, b2, b3}.
Primeiro vejamos produto AXB, que neste caso possui 27 pares ordenados.
 . Portanto, nesse caso temos
. Portanto, nesse caso temos 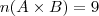 .
.FilipeCaceres escreveu:Desta forma temos um total derelações.
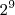 relações possíveis.
relações possíveis.FilipeCaceres escreveu:Agora devemos classificá-los, como:
Injetorasé injetora quando
Sobrejetorasé sobrejetora quando
Bijetoras.é sobrejetora quando f é injetora e sobrejora ao mesmo tempo.



FilipeCaceres escreveu:Acredito que basta fazer isto, para saber a quantidade de funções, façamos o número de elementos de B elevado ao número de elementos de A, assim temos:, ou seja, temos 27 funções.
Ex.:
Observações:
1 - O número de funções não é encontrado da forma com você fez, e sim utliza-se o princípio fundamental da contagem, pois para cada elemento do conjunto A =
{a1; a2; a3} temos três opções, como seuge:
3 x 3 x 3 = 27 funções possíveis.
___ ____ ____
1º 2º 3º
2 - O exemplo acima não é uma função.
Abraço.

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 .
.



