a questão é bem mais simples do que parece...
o quadradro inteiro mede S=
16cm²pois S = l² ==> 4.4 = 16 cm²
pode se calcular tb os 04 triangulos q possuem
base = 2 cm(a altura tb vai ser 02)
(a base é igual a 02, pois se o lado do quadrado é 04
é so subtrair 01 para cada raio q está na mesma reta)
04 -01 -01 ==> base do triangulo = 2 cm
são triangulos isósceles de base 02...
e altura(h) que coincidentemente tb é 02cmpois o centro da figura, é justamente de onde partem todos os triangulos
olhando-se somente para 01 deles se percebe q sua altura corresponde a metade da lateral do quadrado
Com isso cada triangulo tem area =
2 cm²pois S =

=
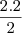
==> S= 2cm²
portanto os 04 triangulos somados valem
8cm²fazendo a subtração do quadrado menos os 04 triangulos, ja temos o resultado parcial
16-8= 8cm²Só falta agora incluir no cálculo, as 04 figuras menores, onde estão os arcos,
na realidade, cada figura desta equivale a 1/4 de circulo,
entao é so raciocinarmos como se fossem um circulo unico
(pois as 04 juntas equivalem a 01 circulo inteiro)
fórmula da area do circulo
S=

S=
 S=
S=  cm²
cm²fica assim então,
praticamente respondida a tua dúvida, so não podendo ser mais preciso,
por eu nao saber quais partes da figura que fazem paete da pergunta em si,
obs,:
a) 8 +\pi --seria os 04 arcos
MAIS os 04 triangulos
b) 8 -\pi --seria a figura q lembra um "X"
MENOS os 04 arcos




 =
= 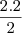 ==> S= 2cm²
==> S= 2cm²

 cm²
cm²
