Olá pessoal,
Não estou conseguindo resolver a questão que segue abaixo, vocês podem me ajudar?
Se f(x) é uma função real e derivável tal que a integral de f '(x) tgx dx é igual a sen³x + C e f(0)= - 1, então f (pi/2) = 1. Verdadeiro ou falso?
Estou encontrando dificuldade para obter a expressão de f(x) a partir da integral de f '(x) tgx dx.


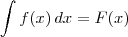 significa que f(x) = F'(x).
significa que f(x) = F'(x).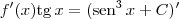 .
. .
. .
.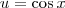 .
.


 , avisa que eu resolvo.
, avisa que eu resolvo.

