 por vinicius cruz » Ter Jun 07, 2011 18:39
por vinicius cruz » Ter Jun 07, 2011 18:39
pretende-se construir um reservatorio de agua de forma prismatica e base quadrada, com capacidade de 686 m³. o m² da cosntrução da tampa da laje de fundo do reservatorio custa o dobro de m² da cosntrução das paredes laterais. Que dimensões deve ter um reservatorio de menor custo?
-
vinicius cruz
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Dom Mar 06, 2011 12:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia civil
- Andamento: cursando
 por LuizAquino » Ter Jun 07, 2011 19:02
por LuizAquino » Ter Jun 07, 2011 19:02
Qual foi exatamente a sua dúvida? Você conseguiu fazer uma ilustração que represente o reservatório? Você sabe como calcular o volume desse reservatório? E a sua área?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por vinicius cruz » Ter Jun 07, 2011 19:16
por vinicius cruz » Ter Jun 07, 2011 19:16
minha duvida é quanto ao uso das formulas...gostaria de ver o desenvolvimento dessa questão pra eu poder entender como interpretar as formulas e aplica-las qunto a maximo e minimo ( no caso dessa o menos custo)
-
vinicius cruz
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Dom Mar 06, 2011 12:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia civil
- Andamento: cursando
 por LuizAquino » Ter Jun 07, 2011 19:27
por LuizAquino » Ter Jun 07, 2011 19:27
Primeiro, note que o volume irá depender de duas variáveis:
- b -- medida dos lados do quadrado da base;
- h -- medida da altura.
A área também irá depender dessas duas variáveis.
Considere que E é o custo na construção da tampa e do fundo do reservatório. Considere também que L é o custo na construção da lateral. Desse modo, o custo C será dado por C = 2E + L.
Mas, como você tem a informação de quanto é o volume, você pode colocar h em função de b (ou o contrário se desejar).
Se você decidir colocar h em função de b, então a sua função custo será algo do tipo C(b).
Desse modo, primeiro você precisará calcular C'(b) = 0 para determinar os pontos críticos de C. Em seguida, você deverá analisar o sinal de C''(b) avaliada nos pontos críticos.
ObservaçãoVocê escreveu:
(...) construção da tampa da laje de fundo (...)
Mas, não seria "
construção da tampa e da laje de fundo"?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por vinicius cruz » Ter Jun 07, 2011 21:06
por vinicius cruz » Ter Jun 07, 2011 21:06
me desculpa
digitei errado
é como está no comentario!!
vc poderia desevolver ela pra mim ...to desesperado aki
queria ver ela pronta
-
vinicius cruz
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Dom Mar 06, 2011 12:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia civil
- Andamento: cursando
 por vinicius cruz » Ter Jun 07, 2011 23:56
por vinicius cruz » Ter Jun 07, 2011 23:56
fazendo os calculos eu achei aresta da base x=7 e altura do solido y=14
bate ai com o q vc fez ??
-
vinicius cruz
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Dom Mar 06, 2011 12:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia civil
- Andamento: cursando
 por LuizAquino » Qua Jun 08, 2011 00:04
por LuizAquino » Qua Jun 08, 2011 00:04
vinicius cruz escreveu:fazendo os calculos eu achei aresta da base x=7 e altura do solido y=14
bate ai com o q vc fez ??
Sim.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por vinicius cruz » Qua Jun 08, 2011 00:14
por vinicius cruz » Qua Jun 08, 2011 00:14
aeeee
obrigado pela força
amanhã tenho prova disso ai .. aprofessora nao teve tempo de dar o assunto com plenitude ai eu tive q correr
obrigado!
-
vinicius cruz
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Dom Mar 06, 2011 12:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia civil
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [derivada] urgente
por telmojc » Qui Mar 22, 2012 07:24
- 3 Respostas
- 2626 Exibições
- Última mensagem por telmojc

Qui Mar 22, 2012 19:04
Funções
-
- Derivada! URGENTE :(
por cardosolucas » Qua Mai 20, 2015 17:08
- 3 Respostas
- 7228 Exibições
- Última mensagem por nakagumahissao

Seg Out 05, 2015 17:28
Cálculo: Limites, Derivadas e Integrais
-
- Ajuda urgente derivada
 por Maisac » Dom Jun 14, 2020 11:57
por Maisac » Dom Jun 14, 2020 11:57
- 1 Respostas
- 11479 Exibições
- Última mensagem por Cleyson007

Qui Jun 25, 2020 14:50
Pedidos
-
- urgente como fazer a derivada
por jayne » Qua Ago 24, 2011 09:24
- 1 Respostas
- 2544 Exibições
- Última mensagem por MarceloFantini

Qua Ago 24, 2011 13:16
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] desta função urgente =(
por Matmenos » Qui Dez 01, 2011 20:33
- 1 Respostas
- 1994 Exibições
- Última mensagem por TheoFerraz

Qui Dez 01, 2011 21:08
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.







 ;
; ;
;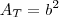 ;
; .
. (nesse contexto,
(nesse contexto,  custa 1 unidade monetária por m² e
custa 1 unidade monetária por m² e  custa 2 unidades).
custa 2 unidades).



 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
