Sub-seção para materiais das disciplinas relacionadas ao cálculo.
Utilize a área de pedidos para outros ou caso a sub-seção da disciplina ainda não possua material.
Provas aplicadas, notas de aulas, listas de exercícios, gabaritos, bibliografias etc.
Regras do fórum
O objetivo desta seção é compartilhar alguns materiais dos próprios alunos do IME-USP, formandos e formados, das disciplinas do curso de Licenciatura em Matemática.
Dentre os materiais, organizados por disciplinas, você encontrará:
Provas aplicadas, notas de aulas, listas de exercícios, gabaritos e bibliografias, além de outros materiais indicados ou fornecidos pelos próprios professores.
A fonte e os créditos do autor devem ser citados sempre que disponíveis.
O intuito deste compartilhamento é favorecer um estudo complementar.
Utilize a seção de pedidos para outros ou caso a sub-seção ainda não possua material.
A pesquisa do fórum facilita a localização de materiais e outros assuntos já publicados.
 por Claytonc » Ter Jun 07, 2011 22:16
por Claytonc » Ter Jun 07, 2011 22:16
estou com duvida neste calculo se alguem puder me ajudar agradeço
![\int_{}^{}(ln(\sqrt[]{3x})/2x)dx
\int_{}^{}{x}^{2}/\sqrt[5]{3-4x} dx
\int_{}^{}2{x}^{2}{e}^{6x/5}dx \int_{}^{}(ln(\sqrt[]{3x})/2x)dx
\int_{}^{}{x}^{2}/\sqrt[5]{3-4x} dx
\int_{}^{}2{x}^{2}{e}^{6x/5}dx](/latexrender/pictures/d26c73c6bbbc172c272ada052759f3bf.png)
-
Claytonc
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Jun 07, 2011 21:03
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia ambiental
- Andamento: cursando
 por LuizAquino » Ter Jun 07, 2011 23:52
por LuizAquino » Ter Jun 07, 2011 23:52
Qual é exatamente a sua dúvida? O que você já tentou fazer?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claytonc » Qua Jun 08, 2011 13:27
por Claytonc » Qua Jun 08, 2011 13:27
Ja, tentei fazer sim, nao consigo chegar a lugar nenhum, nesses calculos, integral devinida blz, entedi, calculo de area, mas nessas ai, nao entendi quando é por partes ou substituicao.Vc vc poder me dar um auxilio eu agradeço muito.
Att
clayton
-
Claytonc
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Jun 07, 2011 21:03
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia ambiental
- Andamento: cursando
 por LuizAquino » Qua Jun 08, 2011 15:53
por LuizAquino » Qua Jun 08, 2011 15:53
Basicamente, será com a prática que você irá perceber quando é interessante usar o método da substituição ou quando é interessante usar o método das partes.
i)

Primeiro, usando propriedades de radiciação e de logaritmos, temos que:

.
Agora, faça a substituição

.
ii)
![\int \frac{x^2}{\sqrt[5]{3-4x}}\,dx \int \frac{x^2}{\sqrt[5]{3-4x}}\,dx](/latexrender/pictures/97d9018f1bfd4b33d2af332c750f9799.png)
Faça a substituição

.
iii)

Faça por partes, sendo que

e
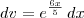
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integrais Indefinidas
por manuel_pato1 » Qui Jan 03, 2013 17:48
- 3 Respostas
- 2636 Exibições
- Última mensagem por manuel_pato1

Ter Jan 08, 2013 15:56
Cálculo: Limites, Derivadas e Integrais
-
- Integrais indefinidas e definidas
por Rose » Qui Abr 23, 2009 11:18
- 2 Respostas
- 5231 Exibições
- Última mensagem por Rose

Qui Abr 23, 2009 16:43
Cálculo: Limites, Derivadas e Integrais
-
- Integrais Indefinidas e definidas 2°EM
por Beik » Sex Out 22, 2010 13:39
- 4 Respostas
- 3228 Exibições
- Última mensagem por Beik

Sáb Out 23, 2010 10:27
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinidas:
por Dethe » Qua Dez 15, 2010 20:48
- 2 Respostas
- 4614 Exibições
- Última mensagem por teabiofeul

Seg Out 05, 2015 08:42
Mensagens Matemáticas
-
- Duvida com Integrais
por MarceloRocks » Seg Dez 03, 2012 00:48
- 3 Respostas
- 4215 Exibições
- Última mensagem por MarceloFantini

Seg Dez 03, 2012 19:43
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{}^{}(ln(\sqrt[]{3x})/2x)dx
\int_{}^{}{x}^{2}/\sqrt[5]{3-4x} dx
\int_{}^{}2{x}^{2}{e}^{6x/5}dx \int_{}^{}(ln(\sqrt[]{3x})/2x)dx
\int_{}^{}{x}^{2}/\sqrt[5]{3-4x} dx
\int_{}^{}2{x}^{2}{e}^{6x/5}dx](/latexrender/pictures/d26c73c6bbbc172c272ada052759f3bf.png)


![\int_{}^{}(ln(\sqrt[]{3x})/2x)dx
\int_{}^{}{x}^{2}/\sqrt[5]{3-4x} dx
\int_{}^{}2{x}^{2}{e}^{6x/5}dx \int_{}^{}(ln(\sqrt[]{3x})/2x)dx
\int_{}^{}{x}^{2}/\sqrt[5]{3-4x} dx
\int_{}^{}2{x}^{2}{e}^{6x/5}dx](/latexrender/pictures/d26c73c6bbbc172c272ada052759f3bf.png)




 .
. .
.![\int \frac{x^2}{\sqrt[5]{3-4x}}\,dx \int \frac{x^2}{\sqrt[5]{3-4x}}\,dx](/latexrender/pictures/97d9018f1bfd4b33d2af332c750f9799.png)
 .
.
 e
e 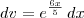 .
.
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.