Oi Kelvin !
Kelvin escreveu:O que é ponto de inflexão?
Pontos de inflexão, são os pontos em que a concavidade da curva muda.
Kelvin escreveu:esse ponto sempre coincide com o zero ou raiz da função?
Não. Na verdade, eles coincidem coma as raízes da segunda derivada da função.
Por exemplo :

A primeira derivada é :

E a segunda derivada é :
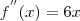
É fácil ver que 0 é a raiz dessa equação.
Portanto 0 é um ponto de inflexão de

Abraços.
Editado pela última vez por
norberto em Ter Mai 24, 2011 17:54, em um total de 1 vez.





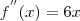



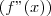 .
. a 0.
a 0. ?
?