 por hevhoram » Qui Jun 02, 2011 16:23
por hevhoram » Qui Jun 02, 2011 16:23
rebeca faz um desafio a leticia: Qual a terça parte de

? . assinale a alternativa que corresponde a resposta correta de leticia
R:
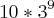
eu fiz assim
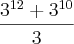
depois cortei um dos 3 mas ficou sem lógica ... como proceder??
-

hevhoram
- Usuário Parceiro

-
- Mensagens: 61
- Registrado em: Qua Jun 02, 2010 11:43
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: informática educacional
- Andamento: formado
 por Fabio Cabral » Qui Jun 02, 2011 17:29
por Fabio Cabral » Qui Jun 02, 2011 17:29
Veja, consegui resolver evidenciando !

Devemos evidenciar a base com menor potência, no caso
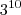
=
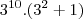
=

=
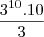
Dividindo por 3 para encontrar a terça parte e cancelando.
=

Abraços !
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Medida da hipotenusa mais terça parte
por dandara » Dom Abr 24, 2016 11:23
- 0 Respostas
- 871 Exibições
- Última mensagem por dandara

Dom Abr 24, 2016 11:23
Trigonometria
-
- Integral da soma/Soma das Integrais.
por Sobreira » Ter Abr 30, 2013 17:41
- 0 Respostas
- 2098 Exibições
- Última mensagem por Sobreira

Ter Abr 30, 2013 17:41
Cálculo: Limites, Derivadas e Integrais
-
- Potências...
por Estela » Dom Mai 04, 2008 22:15
- 3 Respostas
- 2582 Exibições
- Última mensagem por Glauber2012

Sex Mar 23, 2012 21:23
Álgebra Elementar
-
- Potências
por Jhennyfer » Dom Abr 28, 2013 14:15
- 5 Respostas
- 6763 Exibições
- Última mensagem por Cleyson007

Seg Abr 29, 2013 12:03
Teoria dos Números
-
- Potências
por Jhennyfer » Qui Mai 16, 2013 11:31
- 3 Respostas
- 2213 Exibições
- Última mensagem por Victor Gabriel

Qui Mai 16, 2013 13:12
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 ? . assinale a alternativa que corresponde a resposta correta de leticia
? . assinale a alternativa que corresponde a resposta correta de leticia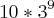
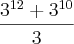 depois cortei um dos 3 mas ficou sem lógica ... como proceder??
depois cortei um dos 3 mas ficou sem lógica ... como proceder??
 ? . assinale a alternativa que corresponde a resposta correta de leticia
? . assinale a alternativa que corresponde a resposta correta de leticia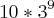
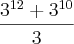 depois cortei um dos 3 mas ficou sem lógica ... como proceder??
depois cortei um dos 3 mas ficou sem lógica ... como proceder??

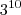
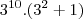

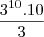 Dividindo por 3 para encontrar a terça parte e cancelando.
Dividindo por 3 para encontrar a terça parte e cancelando.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.