![\lim_{x\rightarrow2}\frac{\sqrt[]{x}+4}{x-2} \lim_{x\rightarrow2}\frac{\sqrt[]{x}+4}{x-2}](/latexrender/pictures/31546c107f215456a034952ac5608b2f.png)
Esse exercício, quando resolvo utilizando racionalização no inicio encontrei como resposta

Porém um amigo meu fez de outro modo substituindo o
![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png) por
por 
ai faz as devidas operações e depois ele faz racionalização no final e encontrou
![-2\sqrt[]{2}-4 -2\sqrt[]{2}-4](/latexrender/pictures/3b5dcc0af932ff7d3cd4692926fc4143.png)
Então gostaria de saber o porque dos resultados distintos, e se alguém puder postar a resolução correta!
Obrigado


![2+\sqrt[]{4} 2+\sqrt[]{4}](/latexrender/pictures/bf523056a0f038a23e2e495fe9b8706e.png) e o denominador tente a zero. Da definição de limite temos que para que o limite exista precisamos que os limites laterais existam e ambos sejam iguais. Observem que de um lado o limite é mais infinito e de outro menos infinito, ou seja os limites laterais não existe(lembre que infinito não é um número) e muito menos são iguais.
e o denominador tente a zero. Da definição de limite temos que para que o limite exista precisamos que os limites laterais existam e ambos sejam iguais. Observem que de um lado o limite é mais infinito e de outro menos infinito, ou seja os limites laterais não existe(lembre que infinito não é um número) e muito menos são iguais.
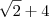 ...
...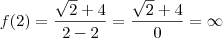
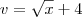 , onde f(x) é sempre maior que 0, pois o menor valor aceitável para a raíz de x é 0 e 0+4 = 4...
, onde f(x) é sempre maior que 0, pois o menor valor aceitável para a raíz de x é 0 e 0+4 = 4...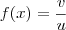
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)