Dos 140 funcionários de uma fábrica, 70 preferem a marca de cigarros FUMAÇA, 80 preferem TOBACO e 30 fumam ambas sem preferências. Sabendo que 20 funcionários não fumam, calcule a probabilidade de que um funcionário, escolhido ao acaso:
a) fume FUMAÇA e TOBACO
b) fume FUMAÇA ou TOBACO
c) fume só FUMAÇA
d) fume só TOBACO
e) fume só FUMAÇA ou só TOBACO
f) não fume nenhuma das duas marcas de cigarro
g) não fume FUMAÇA
h) não fume TOBACO
O número de funcionários não seria 200 em vez de 140? Já que 70 + 80 + 30 + 20 = 200. Se 70 funcionários preferem a marca FUMAÇA, então eles não podem também preferir a marca TOBACO. A preferência deles não seria um evento mutuamente exclusivo? Não acho que a questão esteja errada, só não estou conseguindo entender de que forma elaborar os conjuntos (onde se inersecionam, se algum está contido em outro, etc.). Alguém pode me ajudar?


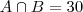

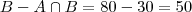
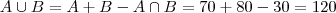


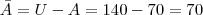
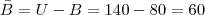
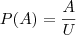 e assim por diante...
e assim por diante...

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)