 por Raphael Feitas10 » Qui Mai 26, 2011 20:02
por Raphael Feitas10 » Qui Mai 26, 2011 20:02
Calcule a e b na proporção

, sabendo-se que

.R: 2 e 6
Brother me ajuda aew fiz ate aqui mas ñ conseguie achar o resultado no soube oq fazer com esse dois aew da equação...
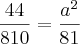
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por FilipeCaceres » Qui Mai 26, 2011 20:11
por FilipeCaceres » Qui Mai 26, 2011 20:11
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Raphael Feitas10 » Qui Mai 26, 2011 22:45
por Raphael Feitas10 » Qui Mai 26, 2011 22:45
FilipeCaceres escreveu:Temos,

brother ñ entendie de onde saio esse 3
Assim temos,

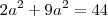
e esse 9 aqui me explica aew parceiro tou confuso aqui...
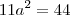
des de já muito obrg por ter me ajudado...


Logo,
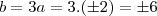
Portanto,

Espero que seja isso.
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Proporção
por Roberta » Ter Jul 14, 2009 17:22
- 2 Respostas
- 3149 Exibições
- Última mensagem por Roberta

Ter Jul 14, 2009 19:53
Desafios Enviados
-
- PROPORÇÃO
por patriciagarciapoa » Qui Nov 05, 2009 16:37
- 1 Respostas
- 1766 Exibições
- Última mensagem por Lucio Carvalho

Qui Nov 05, 2009 17:14
Matemática Financeira
-
- Proporção
por Juliane » Seg Nov 22, 2010 10:32
- 2 Respostas
- 1937 Exibições
- Última mensagem por alexandre32100

Seg Nov 22, 2010 13:38
Álgebra Elementar
-
- Proporção
por Cristina Alves » Qui Fev 03, 2011 21:54
- 2 Respostas
- 2871 Exibições
- Última mensagem por Cristina Alves

Sex Fev 04, 2011 13:41
Álgebra Elementar
-
- Proporção 12
por Raphael Feitas10 » Sex Fev 18, 2011 00:06
- 1 Respostas
- 1438 Exibições
- Última mensagem por Molina

Sex Fev 18, 2011 13:29
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , sabendo-se que
, sabendo-se que  .R: 2 e 6
.R: 2 e 6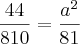

 , sabendo-se que
, sabendo-se que  .R: 2 e 6
.R: 2 e 6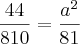



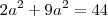
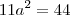


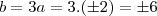


brother ñ entendie de onde saio esse 3
e esse 9 aqui me explica aew parceiro tou confuso aqui...
des de já muito obrg por ter me ajudado...


 .
.
 :
: