Olá Rose!
Uma seção dos sólidos com centro comum pode ser representada por esta figura:
Como você deve saber que o objetivo por aqui não é apenas fornecer a resolução, pois de fato traria pouca contribuição ao estudante, sugiro que você separe o problema em etapas para compreendê-lo.
De início, você precisará saber representar a expressão da área da superfície lateral de um cone. Sem decorar fórmulas, pense em "cortar" e planificar o cone para obter sua área. Há outro tópico no fórum discutindo este procedimento. Revise este assunto!
Pois bem, como os cones estão com as bases justapostas, a área da superfície do sólido será o dobro da expressão que você obteve para a área da superfície lateral de um único cone, OK?
Escreva a expressão para a área da superfície esférica.
Pelo enunciado, estas áreas são iguais! Devemos então impor esta condição.
É importante você fazer este trabalho até aqui.
Em seguida, quando tiver a expressão das áreas igualadas, você terá uma nova etapa: resolver uma
equação biquadrada em
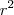
.
A etapa final será escrever as expressões dos volumes citados na razão e substituir
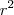
obtido na resolução da equação biquadrada.
Comente seu desenvolvimento e as novas dúvidas!
Bons estudos!


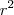 .
.