 por theSinister » Seg Mai 23, 2011 17:11
por theSinister » Seg Mai 23, 2011 17:11
como simplificar:
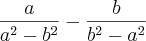
eu sei que o resultado vai dar
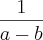
, porém não consegui chegar nesse resultado help-me
-
theSinister
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sáb Abr 23, 2011 18:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Seg Mai 23, 2011 20:27
por Molina » Seg Mai 23, 2011 20:27
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por theSinister » Seg Mai 23, 2011 21:45
por theSinister » Seg Mai 23, 2011 21:45
ainda não consegui entender.
Eu sei que em uma subtração de frações , tira-se o mmc dos denominadores ai ,divide embaixo e multiplica em cima , nesse caso para achar o mmc basta multiplicar os denominadores ficando: a²b²-a^4-b^4+b²a²,, me ajudem ae
-
theSinister
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sáb Abr 23, 2011 18:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Seg Mai 23, 2011 21:54
por Molina » Seg Mai 23, 2011 21:54
Boa noite.
theSinister escreveu:ainda não consegui entender.
Eu sei que em uma subtração de frações , tira-se o mmc dos denominadores ai ,divide embaixo e multiplica em cima , nesse caso para achar o mmc basta multiplicar os denominadores ficando: a²b²-a^4-b^4+b²a²,, me ajudem ae
É isso mesmo, para tirar o mmc dos denominadores eu simplesmente os multipliquei, só que eu não resolvi o produto entre eles, e sim deixei na forma que estavam. Note isto que eu estou falando, quando fiz aqui:
Molina escreveu: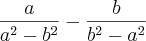
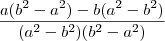
Qualquer dúvida, informe, que eu explico passo a passo.
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por theSinister » Seg Mai 23, 2011 22:11
por theSinister » Seg Mai 23, 2011 22:11
bom se o mmc entre os denominadores é a²b²-a^4-b^4+b²a², eu deveria dividir por a-b² e multiplicar por a certo? depois dividir por b²-a² e multiplicar por b ,mas ainda não entendi pq q ficou a (b²-a²)-b(a²-b²)/ (a²-b²)(b²-a²)
-
theSinister
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sáb Abr 23, 2011 18:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Seg Mai 23, 2011 22:30
por Molina » Seg Mai 23, 2011 22:30
theSinister escreveu:bom se o mmc entre os denominadores é a²b²-a^4-b^4+b²a², eu deveria dividir por a-b² e multiplicar por a certo? depois dividir por b²-a² e multiplicar por b ,mas ainda não entendi pq q ficou a (b²-a²)-b(a²-b²)/ (a²-b²)(b²-a²)
Sim, este valor que você está dizendo ser o mmc de fato é, porém você "abriu" o produto

e eu não. Ambos representam o mesmo valor, porém, eu preferi deixar ele da forma que está e não da forma que você fez (fazendo a distributiva termo a termo). Esta opção que eu fiz em deixar ele da forma fatorada

foi uma das opções que achei melhor para chegar no resultado.
Perceba que:


Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por theSinister » Seg Mai 23, 2011 22:34
por theSinister » Seg Mai 23, 2011 22:34
brigadão cara , agora eu entendi vlw , o resto ta d boa .
-
theSinister
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sáb Abr 23, 2011 18:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Divisão de polinômios
por manuoliveira » Dom Nov 14, 2010 14:00
- 1 Respostas
- 2596 Exibições
- Última mensagem por VtinxD

Seg Nov 15, 2010 01:13
Polinômios
-
- Divisão de Polinômios
por -civil- » Seg Mai 30, 2011 20:31
- 3 Respostas
- 2439 Exibições
- Última mensagem por -civil-

Seg Mai 30, 2011 21:20
Cálculo: Limites, Derivadas e Integrais
-
- Divisão de Polinômios
por Claudin » Qua Ago 03, 2011 20:25
- 3 Respostas
- 2189 Exibições
- Última mensagem por Claudin

Qui Ago 04, 2011 15:46
Polinômios
-
- Divisão de polinômios
por Gaules » Qua Out 19, 2011 16:47
- 0 Respostas
- 1416 Exibições
- Última mensagem por Gaules

Qua Out 19, 2011 16:47
Polinômios
-
- Divisão de polinômios
por Pri Ferreira » Ter Mai 08, 2012 21:28
- 1 Respostas
- 1400 Exibições
- Última mensagem por DanielFerreira

Ter Mai 08, 2012 23:02
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
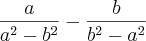 eu sei que o resultado vai dar
eu sei que o resultado vai dar 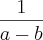 , porém não consegui chegar nesse resultado help-me
, porém não consegui chegar nesse resultado help-me
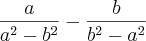 eu sei que o resultado vai dar
eu sei que o resultado vai dar 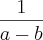 , porém não consegui chegar nesse resultado help-me
, porém não consegui chegar nesse resultado help-me
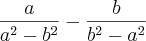
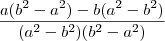

![\frac{(a+b)[a(b-a) - b(a-b)]}{(a+b)^2(a-b)(b-a)} \frac{(a+b)[a(b-a) - b(a-b)]}{(a+b)^2(a-b)(b-a)}](/latexrender/pictures/cdd99a3fe6b34d3bbb0962c84f13d983.png)
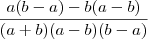


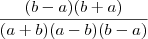
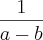





 e eu não. Ambos representam o mesmo valor, porém, eu preferi deixar ele da forma que está e não da forma que você fez (fazendo a distributiva termo a termo). Esta opção que eu fiz em deixar ele da forma fatorada
e eu não. Ambos representam o mesmo valor, porém, eu preferi deixar ele da forma que está e não da forma que você fez (fazendo a distributiva termo a termo). Esta opção que eu fiz em deixar ele da forma fatorada  foi uma das opções que achei melhor para chegar no resultado.
foi uma das opções que achei melhor para chegar no resultado.


