Temos
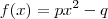
e
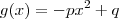
Para encontrar o ponto de intersecção do gráfico com as coordenadas, basta calcular

Para f(x) temos:

Para g(x) temos:

A distância de
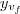
até
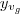
corresponde a uma das diagonais, para encontrar a outra diagonal devemos encontrar a intersecção entre os gráficos,para isso façamos f(x)=g(x),então temos,

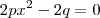
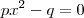
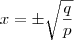
Sabendo as diagonais é fácil calcular a área de um quadrilátero, supondo que "a" e "b" são nossas diagonais e que

seja o angulo entre elas temos que a área do nosso quadrilátero é calculo por:
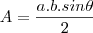
Agora observe que tanto os valores de

quanto os valores

estão sobre os eixo das coordenadas e abscissas respectivamente, e desta forma o nosso valor de
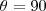
Assim temos,
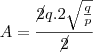
Portanto,
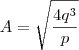
Espero que seja isso.
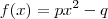 e
e 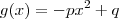 , onde p e q são números reais não nulos. A área do quadrilátero que tem como vértices os pontos de intersecção dos gráficos com os eixos coordenados vale:
, onde p e q são números reais não nulos. A área do quadrilátero que tem como vértices os pontos de intersecção dos gráficos com os eixos coordenados vale: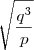
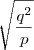
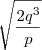
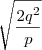
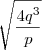
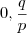 . Mas agora não sei continuar
. Mas agora não sei continuar




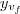 até
até 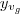 corresponde a uma das diagonais, para encontrar a outra diagonal devemos encontrar a intersecção entre os gráficos,para isso façamos f(x)=g(x),então temos,
corresponde a uma das diagonais, para encontrar a outra diagonal devemos encontrar a intersecção entre os gráficos,para isso façamos f(x)=g(x),então temos,
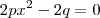
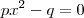
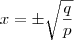
 seja o angulo entre elas temos que a área do nosso quadrilátero é calculo por:
seja o angulo entre elas temos que a área do nosso quadrilátero é calculo por: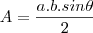
 estão sobre os eixo das coordenadas e abscissas respectivamente, e desta forma o nosso valor de
estão sobre os eixo das coordenadas e abscissas respectivamente, e desta forma o nosso valor de 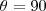
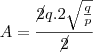
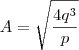

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.