Meu nome é Jorge Rodrigo e estou cursando duas disciplinas (que ficaram pendentes no meu primeiro período, atualmente estou no segundo, mas cursando ainda essas disciplinas) do primeiro período de matemática na Rural de Nova Iguaçu e gostaria, se possível, que me ajudassem a resolver uma questão da minha lista de exercícios.... ai vai:
![\sqrt[]{{\left[ \frac{1}{2}*\left(\frac{a}{b} \right)^\frac{-1}{2}-\frac{1}{2}*\left\left(\frac{b}{a} \right)^\left(\frac{-1}{2} \right)\right]}^{-2}+1} \sqrt[]{{\left[ \frac{1}{2}*\left(\frac{a}{b} \right)^\frac{-1}{2}-\frac{1}{2}*\left\left(\frac{b}{a} \right)^\left(\frac{-1}{2} \right)\right]}^{-2}+1}](/latexrender/pictures/cc8459cee2bc3bb67e99a95686551072.png)
O gabarito é: a + b/|a - b|.
Abaixo segue minha resolução:
Aplicando propriedades das potências, temos:
![\Rightarrow\sqrt[]{{\left[ \frac{1}{2}*\sqrt[]{\frac{b}{a}} -\frac{1}{2}*\sqrt[]{\frac{a}{b}}\right]}^{-2}+1} \Rightarrow\sqrt[]{{\left[ \frac{1}{2}*\sqrt[]{\frac{b}{a}} -\frac{1}{2}*\sqrt[]{\frac{a}{b}}\right]}^{-2}+1}](/latexrender/pictures/0a448f70a0da879e43e44062446c83d5.png)
Introduzindo um fator no radical, temos:
![\Rightarrow\sqrt[]{{\left[\frac{\sqrt[]{b}}{\sqrt[]{4a}}-\frac{\sqrt[]{a}}{\sqrt[]{4b}}\right]}^{-2}+1} \Rightarrow\sqrt[]{{\left[\frac{\sqrt[]{b}}{\sqrt[]{4a}}-\frac{\sqrt[]{a}}{\sqrt[]{4b}}\right]}^{-2}+1}](/latexrender/pictures/f35583abd27a20b0ca20db779c9952d7.png)
Aplicando propriedades da potências, temos:
![\Rightarrow\sqrt[]{{\left[\frac{\sqrt[]{4a}}{\sqrt[]{b}}-\frac{\sqrt[]{4b}}{\sqrt[]{a}}\right]}^{2}+1} \Rightarrow\sqrt[]{{\left[\frac{\sqrt[]{4a}}{\sqrt[]{b}}-\frac{\sqrt[]{4b}}{\sqrt[]{a}}\right]}^{2}+1}](/latexrender/pictures/923fd2a2fa263835e1f5ad710cdeb531.png)
Igualando os denominadores, temos:
![\Rightarrow\sqrt[]{{\left[\frac{{2a}}{\sqrt[]{ba}}-\frac{{2b}}{\sqrt[]{ba}}\right]}^{2}+1} \Rightarrow\sqrt[]{{\left[\frac{{2a}}{\sqrt[]{ba}}-\frac{{2b}}{\sqrt[]{ba}}\right]}^{2}+1}](/latexrender/pictures/de8eaef099f9e9fd692bcdf2bfa46f6b.png)
Aplicando produtos notáveis, temos:
![\Rightarrow\sqrt[]{\frac{{4a}^{2}}{ba}-\frac{8ab}{ba}+\frac{{4b}^{2}}{ba}+1} \Rightarrow\sqrt[]{\frac{{4a}^{2}}{ba}-\frac{8ab}{ba}+\frac{{4b}^{2}}{ba}+1}](/latexrender/pictures/89d6dce4828e46fd8999e688b5863452.png)
Resolvendo a expressão, temos:
![\Rightarrow\sqrt[]{{4a}^{2}-{7ab}+{4b}^{2}} \Rightarrow\sqrt[]{{4a}^{2}-{7ab}+{4b}^{2}}](/latexrender/pictures/a3730019b6598830bcff2ddccb9b28c3.png)
... consegui chegar até aqui!




![\Rightarrow\sqrt[]{{\left[\frac{\sqrt[]{b}*\sqrt{4b}}{\sqrt[]{4a}*\sqrt{4b}}-\frac{\sqrt[]{a}*\sqrt{4a}}{\sqrt[]{4b}*\sqrt{4a}}\right]}^{-2}+1} \Rightarrow\sqrt[]{{\left[\frac{\sqrt[]{b}*\sqrt{4b}}{\sqrt[]{4a}*\sqrt{4b}}-\frac{\sqrt[]{a}*\sqrt{4a}}{\sqrt[]{4b}*\sqrt{4a}}\right]}^{-2}+1}](/latexrender/pictures/0600ec71f29df8558c51516eb857aa79.png)
![\Rightarrow\sqrt[]{{\left[\frac{2 |b|}{\sqrt[]{16ab}}-\frac{2 |a|}{\sqrt{16ab}}\right]}^{-2}+1} \Rightarrow\sqrt[]{{\left[\frac{2 |b|}{\sqrt[]{16ab}}-\frac{2 |a|}{\sqrt{16ab}}\right]}^{-2}+1}](/latexrender/pictures/465185daca35990c720e877c88468f43.png)
![\Rightarrow\sqrt[]{{\left[\frac{2 |b| - 2 |a|}{\sqrt[]{16ab}}\right]}^{-2}+1} \Rightarrow\sqrt[]{{\left[\frac{2 |b| - 2 |a|}{\sqrt[]{16ab}}\right]}^{-2}+1}](/latexrender/pictures/6ad42f89b92d4d0ce971df9d37646305.png)
![\Rightarrow\sqrt[]{{\left[\frac{\sqrt[]{16ab}}{2 |b| - 2 |a|}\right]}^{2}+1} \Rightarrow\sqrt[]{{\left[\frac{\sqrt[]{16ab}}{2 |b| - 2 |a|}\right]}^{2}+1}](/latexrender/pictures/4c891548f83c235294929b42ec711696.png)
![\Rightarrow\sqrt[]{{\frac{16ab}{(2 |b| - 2 |a|)^2 }}+1} \Rightarrow\sqrt[]{{\frac{16ab}{(2 |b| - 2 |a|)^2 }}+1}](/latexrender/pictures/56e465f9e25393abb51c94dc1fb7d939.png)
![\Rightarrow\sqrt[]{{\frac{16ab+(2 |b| - 2 |a|)^2}{(2 |b| - 2 |a|)^2 }}} \Rightarrow\sqrt[]{{\frac{16ab+(2 |b| - 2 |a|)^2}{(2 |b| - 2 |a|)^2 }}}](/latexrender/pictures/8a6f5be71e7e3c0030a3cc5b35ea0cee.png)



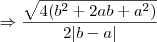

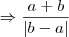

![{\left[ \frac{m}{n} \right]}^{-2} {\left[ \frac{m}{n} \right]}^{-2}](/latexrender/pictures/bffe43074b594a2a0bb87ff307038c4a.png) =
= ![{\left[ \frac{n}{m} \right]}^{2} {\left[ \frac{n}{m} \right]}^{2}](/latexrender/pictures/04dd5e7bc310f45c15c6247ffcb3ae39.png)
![{\left[ \frac{m}{n} + \frac{o}{p} \right]}^{-2} {\left[ \frac{m}{n} + \frac{o}{p} \right]}^{-2}](/latexrender/pictures/b5d3156ff01b2a32acb1bb7e52b57918.png) =
= ![{\left[ \frac{n}{m} + \frac{p}{o} \right]}^{2} {\left[ \frac{n}{m} + \frac{p}{o} \right]}^{2}](/latexrender/pictures/449af5001ade0d4cb640c2f165c8c4d6.png)
![{\left[ \frac{pm + no}{np} \right]}^{-2} {\left[ \frac{pm + no}{np} \right]}^{-2}](/latexrender/pictures/e6cc80305faed4eb9ebe29c33b6c4073.png)
![{\left[ \frac{np}{pm + no} \right]}^{2} {\left[ \frac{np}{pm + no} \right]}^{2}](/latexrender/pictures/7d5143947394da00efac7864b85c2ea3.png)

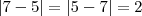
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)