 por raimundoocjr » Sáb Mai 14, 2011 15:32
por raimundoocjr » Sáb Mai 14, 2011 15:32
01. Uma torre de comunicações conta com 5 bandeiras sinalizadoras, e as mensagens são enviadas quando uma ou mais bandeiras são hasteadas. Quantas mensagens distintas podem ser enviadas?
a) 125
b) 245
c) 325
d) 420
e) 640
A priori não tenho uma base para início.
02. A mala do professor Niltinho tem um cadeado cujo segredo é uma combinação com 5 algarismos, cada um dos quais podendo varias de 0 a 9. Ele esqueceu a combinação que escolhera como segredo, mas sabe que atende às seguintes comdições:
I) Se o primeiro algarismo é ímpar, então o último algarismo também é ímpar;
II) Se o primeiro algarismo é par, então o último algarismo é igual ao primeiro;
III) A soma do segundo e terceiro algarismos é igual a 5.
Quantas combinações diferentes atendem às condições estabelecidas pelo professor Niltrinho?
a) 1.175
b) 1.320
c) 1.640
d) 1.800
e) 1.940
Tentei resolvê-la assim;
Considerando o inciso I: 5._._.5 (sendo os travessões completados pelas combinações: 0 e 5; 1 e 4; 2 e 3; 3 e 2; 4 e 1; 5 e 0, respectivamente). Em síntese será o produto de 6 (combinações para a soma ser 5) e 25 (inciso I). Já com o inciso III tem-se: 5._._.1, utilizando as mesmas combinações já citadas o resultado é o produto de 5 (inciso III) e 6 (combinações). Somando 150 e 30 obtém-se 180, não correspondendo nenhuma alternativa com isto.
Por favor ajudem-me, desde já obrigado.
-
raimundoocjr
-
 por FilipeCaceres » Sáb Mai 14, 2011 17:25
por FilipeCaceres » Sáb Mai 14, 2011 17:25
Vou postar a primeira, depois eu vejo o outro e alguém resolve.
Observe que você pode usar ou apenas 1 ou 2,3,4,5, desta forma usando o princípio aditivo podemos escrever o seguinte:
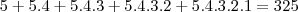
mensagens.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por raimundoocjr » Seg Mai 16, 2011 20:58
por raimundoocjr » Seg Mai 16, 2011 20:58
Obrigado por ajudar na primeira questão. A número 2 ainda está me deixando confuso. Se alguém puder ajudar é bem-vindo.
-
raimundoocjr
-
 por FilipeCaceres » Seg Mai 16, 2011 21:33
por FilipeCaceres » Seg Mai 16, 2011 21:33
Ainda bem que você "ressuscitou" esta questão,pois eu já havia me esquecido dela.
Vamos para a questão.
Façamos os cinco risquinhos então:
_._._._._
IMPARPara o primeiro e o último temos 5(1,3,5,7,9)
5._._._.5
A soma do segundo e terceiro é igual a 5,logo so podemos colocar os seguinte números (0,1,2,3,4,5), desta forma temos 6 possibilidades para o primeiro e apenas 1 para o segundo.
5.6.1._.5
Para nosso quarto número temos 10 possibilidades,visto que não foi nos dado nenhuma restrição.
5.6.1.10.5 =1800
PARPara os número pares teremos,
5.6.1.10.1=300
Observe que coloquei 1 no último pois ao escolher um dos 5 números pares para o primeiro so nos resta uma possibilidade para o último,pois deve ser igual.
Desta forma temos que o total de possibilidades é:
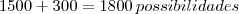
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por raimundoocjr » Ter Mai 17, 2011 17:27
por raimundoocjr » Ter Mai 17, 2011 17:27
Obrigado. De facto, o problema era a análise das restrições impostas.
-
raimundoocjr
-
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Análise Combinatória - "Pesquisa, Maria L. e Nacionalidades"
por raimundoocjr » Ter Mai 17, 2011 17:43
- 0 Respostas
- 2540 Exibições
- Última mensagem por raimundoocjr

Ter Mai 17, 2011 17:43
Estatística
-
- Análise Combinatória - "Time de Basquete"
por raimundoocjr » Seg Set 06, 2010 19:57
- 2 Respostas
- 1525 Exibições
- Última mensagem por raimundoocjr

Ter Set 07, 2010 14:15
Estatística
-
- Análise Combinatória - "Torcedores"
por raimundoocjr » Sex Nov 05, 2010 22:44
- 2 Respostas
- 1081 Exibições
- Última mensagem por raimundoocjr

Dom Nov 07, 2010 13:00
Estatística
-
- Sistemas Lineares: "a, b e c" como "soluções".
por allendy » Qua Set 08, 2010 20:28
- 2 Respostas
- 11303 Exibições
- Última mensagem por allendy

Qua Set 08, 2010 20:37
Sistemas de Equações
-
- [LIMITES] Limite de Raiz "m" de "infinito"
por antonelli2006 » Sáb Set 17, 2011 05:56
- 5 Respostas
- 9192 Exibições
- Última mensagem por LuizAquino

Dom Set 18, 2011 10:08
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

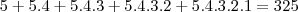 mensagens.
mensagens.
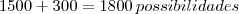


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.