Concordo... rs
Mas, apesar de matriz ser trabalhoso, pra equação da reta é uma matriz pequena... eu prefiro o método da substituição.... mas, pra fazer por matriz, tendo ponto A(xa,ya) e B(xb,yb), voce monta:
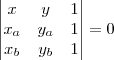
Sai bonitinha a equação da reta.... no formato ax+by+c...
Muita gente subvaloriza as matrizes... eu mesmo fiz isso durante muito tempo... e continuo não usando esse método pra praticamente nada.... entretanto, é um algoritmo muito eficiente, desde que se entenda o porque de cada valor que comporá a matriz e teremos o resultado de forma fácil... não necessariamente simples, mas fácil.... como Briot-Ruffini



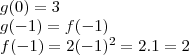
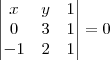
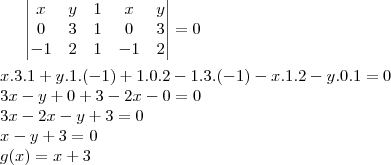
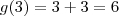

 é uma reta, logo
é uma reta, logo  , com a e b a determinar. Como
, com a e b a determinar. Como 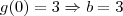 . Temos também que
. Temos também que  . Assim,
. Assim,  e portanto
e portanto 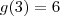 .
.




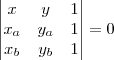






 , avisa que eu resolvo.
, avisa que eu resolvo.

