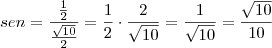por Guilherme Carvalho » Sex Mai 13, 2011 12:24
por Guilherme Carvalho » Sex Mai 13, 2011 12:24
Num retângulo de lados 1cm e 3cm, o menor seno do ângulo formado pelas diagonais é:
a)4/5
b)3/5
c)1/5
d)1/3
e)2/5
-
Guilherme Carvalho
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Mar 03, 2011 12:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecatrônica
- Andamento: cursando
 por carlosalesouza » Sex Mai 13, 2011 16:47
por carlosalesouza » Sex Mai 13, 2011 16:47
Primeiramente, encontrando as diagonais:

Agora, sabemos que o menor seno pertence ao ângulo que possua menor cateto oposto, ou seja, pegaremos o ângulo voltado para o lado menor...
Contudo, para termos um triângulo retângulo, vamos cortá-lo ao meio, então seu lado oposto será a metade do ângulo original...
Sabemos que as diagonais se cruzam em seu ponto médio... Assim as medidas desse triângulo retângulo são:

Assim:

Pra encontrar o seno, basta b/a... mas esse ângulo é a metade do ângulo que queremos... então sen(2x)
E sabemos que sen(2x) = 2(senx.cosx)
Então precisamos achar o coseno tbm...
O seno:
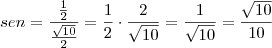
O coseno:

Agora podemos fazer

Portanto, a respostá é B
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão (MACKENZIE)
por Carolziiinhaaah » Qua Jun 16, 2010 12:04
- 1 Respostas
- 3446 Exibições
- Última mensagem por Elcioschin

Qua Jun 16, 2010 13:32
Progressões
-
- Questão da MACKENZIE
 por Kelvin Brayan » Dom Mar 27, 2011 16:18
por Kelvin Brayan » Dom Mar 27, 2011 16:18
- 2 Respostas
- 8330 Exibições
- Última mensagem por Kelvin Brayan

Dom Mar 27, 2011 16:34
Funções
-
- (Mackenzie)
por my2009 » Sex Jan 28, 2011 21:28
- 1 Respostas
- 2689 Exibições
- Última mensagem por 0 kelvin

Sáb Jan 29, 2011 18:57
Logaritmos
-
- (Mackenzie) P.A. com P.G.
por Rafael16 » Sáb Ago 04, 2012 14:19
- 3 Respostas
- 10071 Exibições
- Última mensagem por MarceloFantini

Qui Set 13, 2012 10:20
Progressões
-
- Mackenzie
por Maria Livia » Qua Fev 27, 2013 22:29
- 1 Respostas
- 33667 Exibições
- Última mensagem por Cleyson007

Qua Fev 27, 2013 22:41
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.