 por jamiel » Sex Mai 13, 2011 15:42
por jamiel » Sex Mai 13, 2011 15:42
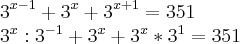
Não consigo passa daí, tentei reduzir os termos, mas não deu jeito. Alguém pra dar uma dica?
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por carlosalesouza » Sex Mai 13, 2011 16:00
por carlosalesouza » Sex Mai 13, 2011 16:00
Jamiel... mais uma vez o mesmo passo em falso... kkk
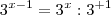
... ok?
Depois de fazer essa decomposição, basta substituir

por uma variável qualquer e encontrar a resposta...
Desenvolve e posta aí pra gente dar uma olhada...
Um abração
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
 por jamiel » Sex Mai 13, 2011 16:49
por jamiel » Sex Mai 13, 2011 16:49
Putz! Sério, não consigo. Deve ser alguma propriedade q não tow encaixando. Tow quase desistindo dessa!
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por MarceloFantini » Sex Mai 13, 2011 17:01
por MarceloFantini » Sex Mai 13, 2011 17:01
Jamiel, diga o que

quer dizer pra você?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por carlosalesouza » Sex Mai 13, 2011 17:15
por carlosalesouza » Sex Mai 13, 2011 17:15
não se apavora meu caro... é tudo bem tranquilo...
Vc só precisa analisar as relações entre os elmentos da equação...
Procura expor sua dúvida de forma mais completa...
Sei que não é o que vc ta procurando... dá pra ver que vc estuda com empenho... mas, a gente te passar a resolução não vai te ajudar tanto quanto se vc mesmo tentar encontrar a resposta, identificando pra gente qual é a sua dificuldade nesse problema...
Um abraço
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
 por jamiel » Sex Mai 13, 2011 17:34
por jamiel » Sex Mai 13, 2011 17:34
Ok. Vamos lá!
3^x/3^1 + 3^x + 3^x*3^1 = 351
Eu sei q um "3^x" tem ficar intácto, pois ele mostrará o valor de x. O 351 será dividido por algum valor do lado esquerdo ser reduzido. Já q o 351 não pode ser reduzido a base 3. Seria, mais ou menos, esse raciocínio?
1/3 + 3 = 3*3 +1 = "10/3"
10/3*3^x +3^x +3^x = 351
Tá complicado essa pra mim!
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por MarceloFantini » Sex Mai 13, 2011 19:40
por MarceloFantini » Sex Mai 13, 2011 19:40
Seja

. Então a equação na nova variável fica
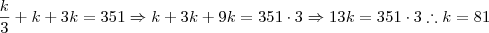
. Portanto,
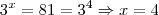
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por jamiel » Sex Mai 13, 2011 20:27
por jamiel » Sex Mai 13, 2011 20:27
Meu Deus! Vou partir para função exponencial q é o q vai cair na minha prova de matemática. rsrsrs
Equação exponencial é meio complicadinho, é q tow sem tempo para me dedicar a ela um pouquinho.
Deixa v se entendi:
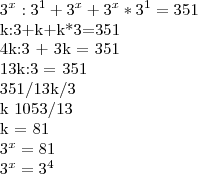
É q eu também tenho q me ater ao conceito. Equação e Função são propostas diferentes, eu sempre acabo confundindo-as!
vlw brow...
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação Exponencial - Problema 2
por jamiel » Seg Mai 09, 2011 18:58
- 7 Respostas
- 2952 Exibições
- Última mensagem por jamiel

Seg Mai 09, 2011 22:53
Sistemas de Equações
-
- Equação Exponencial - Problema 3
por jamiel » Ter Mai 10, 2011 14:03
- 2 Respostas
- 1823 Exibições
- Última mensagem por jamiel

Qua Mai 11, 2011 00:30
Sistemas de Equações
-
- Equação Exponencial - Problema 4
por jamiel » Sex Mai 13, 2011 03:00
- 7 Respostas
- 4055 Exibições
- Última mensagem por jamiel

Sex Mai 13, 2011 15:24
Sistemas de Equações
-
- Problema Com Inequação do Exponencial
por chenz » Sáb Jun 19, 2010 17:13
- 2 Respostas
- 1772 Exibições
- Última mensagem por chenz

Dom Jun 20, 2010 12:35
Funções
-
- Função Exponencial - problema 1
por jamiel » Sáb Mai 14, 2011 15:40
- 6 Respostas
- 2726 Exibições
- Última mensagem por jamiel

Dom Mai 15, 2011 10:40
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
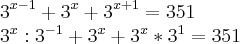

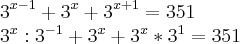

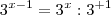 ... ok?
... ok? por uma variável qualquer e encontrar a resposta...
por uma variável qualquer e encontrar a resposta...




 . Então a equação na nova variável fica
. Então a equação na nova variável fica 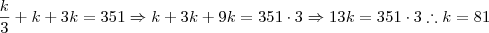 . Portanto,
. Portanto, 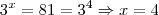 .
.

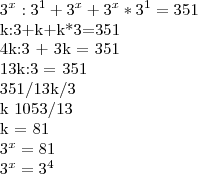

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.