 por Fernanda Lauton » Ter Mai 10, 2011 16:54
por Fernanda Lauton » Ter Mai 10, 2011 16:54
Bem, eu sei que ao se resolver expressões numéricas a multiplicação e a divisão têm a mesma prioridade para resolução, Então na expressão:
(

1)
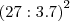
ou 2)
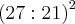
= 1.63

Se as duas formas são possíveis porque deram resultados diferentes! Onde foi que eu errei?

Onde foi que errei novamente?
Fernanda lauton
-
Fernanda Lauton
- Usuário Parceiro

-
- Mensagens: 58
- Registrado em: Seg Mar 29, 2010 17:21
- Localização: Minas Gerais
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Biologia
- Andamento: formado
 por rafaela amadeu » Ter Mai 10, 2011 17:58
por rafaela amadeu » Ter Mai 10, 2011 17:58
1° vc tem q resolver a potencia:
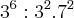
dai pra frente eh simples
diminui potencias de bases iguais
resolvendo fica assim


resolvendo a potencia fica
81:49
-
rafaela amadeu
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Mai 10, 2011 17:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: ensino medio
- Andamento: formado
 por Fernanda Lauton » Ter Mai 10, 2011 18:50
por Fernanda Lauton » Ter Mai 10, 2011 18:50
Mas primeiro tem q resolver o que tem dentro do parenteses naum é :S
na verdade a resposta do livro foi a segunda que eu postei
Editado pela última vez por
Fernanda Lauton em Ter Mai 10, 2011 18:53, em um total de 1 vez.
Fernanda lauton
-
Fernanda Lauton
- Usuário Parceiro

-
- Mensagens: 58
- Registrado em: Seg Mar 29, 2010 17:21
- Localização: Minas Gerais
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Biologia
- Andamento: formado
 por Fernanda Lauton » Ter Mai 10, 2011 18:51
por Fernanda Lauton » Ter Mai 10, 2011 18:51
...
Fernanda lauton
-
Fernanda Lauton
- Usuário Parceiro

-
- Mensagens: 58
- Registrado em: Seg Mar 29, 2010 17:21
- Localização: Minas Gerais
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Biologia
- Andamento: formado
 por MarceloFantini » Ter Mai 10, 2011 19:37
por MarceloFantini » Ter Mai 10, 2011 19:37
Sua notação é confusa, faltam parenteses para esclarecer. Veja que não dá pra saber se é

ou
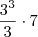
. Também não entendo as outras questões.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equações elementares
por douglasjro » Seg Jan 10, 2011 19:38
- 6 Respostas
- 2785 Exibições
- Última mensagem por douglasjro

Ter Jan 11, 2011 19:43
Álgebra Elementar
-
- Dúvida sobre operações entre conjuntos - complementar
por Fernanda Lauton » Sáb Out 09, 2010 21:18
- 3 Respostas
- 2624 Exibições
- Última mensagem por MarceloFantini

Sáb Out 09, 2010 23:18
Funções
-
- operações de conjuntos
por Sergio Ribeiro Alves » Qui Fev 14, 2008 10:40
- 1 Respostas
- 4131 Exibições
- Última mensagem por admin

Qui Fev 14, 2008 16:21
Álgebra Elementar
-
- Matriz operações
por DanielRJ » Qui Set 09, 2010 18:06
- 5 Respostas
- 3801 Exibições
- Última mensagem por DanielRJ

Sex Set 10, 2010 17:15
Matrizes e Determinantes
-
- Operações com Conjuntos
por tertulia » Qui Dez 30, 2010 20:17
- 0 Respostas
- 1411 Exibições
- Última mensagem por tertulia

Qui Dez 30, 2010 20:17
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

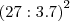 ou 2)
ou 2) 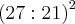 = 1.63
= 1.63



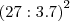 ou 2)
ou 2) 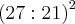 = 1.63
= 1.63


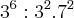





 ou
ou 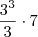 . Também não entendo as outras questões.
. Também não entendo as outras questões.
