 por Guilherme Carvalho » Ter Mai 10, 2011 17:19
por Guilherme Carvalho » Ter Mai 10, 2011 17:19
Galera me ajuda ai não estou conseguindo fazer essas
O valor real
a e o menor entre os valores de
x que satisfazem a equação
![2{log}_{2}(1+\sqrt[2]{2x})-{log}_{2}(\sqrt[2]{2x})=3 2{log}_{2}(1+\sqrt[2]{2x})-{log}_{2}(\sqrt[2]{2x})=3](/latexrender/pictures/f0626009da5a28929dc47587076ba7b8.png)
.Então,

é igual a:
a)1/4
b)1/2
c)1
d)3/2
e)2
Agradeço desde ja
-
Guilherme Carvalho
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Mar 03, 2011 12:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecatrônica
- Andamento: cursando
 por carlosalesouza » Qui Mai 12, 2011 14:53
por carlosalesouza » Qui Mai 12, 2011 14:53
Olá... não há nenhum erro na transcrição?
Eu fiz e refiz esse exercício e não cheguei em nenhuma das alternativas... a resposta que encontro sempre é
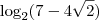
, que dá aproximadamente 0,425...
Um abraço
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
 por Guilherme Carvalho » Sex Mai 13, 2011 12:11
por Guilherme Carvalho » Sex Mai 13, 2011 12:11
Cara ta igualzinho aqui no livro.... a resposta do gabarito é b)1/2
-
Guilherme Carvalho
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Mar 03, 2011 12:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecatrônica
- Andamento: cursando
 por carlosalesouza » Sex Mai 13, 2011 14:18
por carlosalesouza » Sex Mai 13, 2011 14:18
Eu devo estar perdendo algum detalhe.... a solução que eu encontrei é meio longa... agora não tem como eu postar ela aqui...
Mas posto ainda hoje... dai a gente pode analisar o que eu estou deixando passar... rs
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
 por Guilherme Carvalho » Sex Mai 13, 2011 14:34
por Guilherme Carvalho » Sex Mai 13, 2011 14:34
blz posta ai. pq essa questão ta mto foda
-
Guilherme Carvalho
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Mar 03, 2011 12:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecatrônica
- Andamento: cursando
 por carlosalesouza » Sex Mai 13, 2011 15:50
por carlosalesouza » Sex Mai 13, 2011 15:50
Vou postar em partes.... rs
temos:
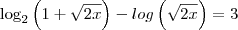
Pelas propriedades do logaritmo:
log(a)+log(b) = log(a.b)
log(a)-log(b) = log(a/b)
Então:
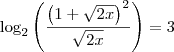
Agora começamos a desenvolver:

sabemos então, que:

Elevamos ambos os lados ao quadrado:
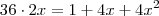
Dividimos ambos os lados por 4:

Temos uma equação de segundo grau, que nos dará
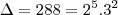
, nos dando uma raíz

...
pegamos logo a raíz negativa, que vai nos dar um valor menor de x:

Esse será nosso valor de a... vamos inseri-lo, então, na próxima sentença:

Dividindo ambos por 3:

E foi até onde eu cheguei... to batendo cabeça ver se vou além disso... rs
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão da Fuvest
por Kelvin Brayan » Qua Mar 02, 2011 11:56
- 2 Respostas
- 4133 Exibições
- Última mensagem por Kelvin Brayan

Qua Mar 02, 2011 13:23
Álgebra Elementar
-
- Questão Fuvest
 por Alex Rom » Qua Mar 30, 2011 11:38
por Alex Rom » Qua Mar 30, 2011 11:38
- 2 Respostas
- 3622 Exibições
- Última mensagem por Alex Rom

Qua Mar 30, 2011 12:07
Geometria Plana
-
- Questão da Fuvest
por my2009 » Qua Mar 30, 2011 10:00
- 4 Respostas
- 3018 Exibições
- Última mensagem por FilipeCaceres

Qua Mar 30, 2011 11:18
Estatística
-
- Questão da Fuvest
 por Kelvin Brayan » Seg Abr 18, 2011 17:11
por Kelvin Brayan » Seg Abr 18, 2011 17:11
- 2 Respostas
- 1723 Exibições
- Última mensagem por Kelvin Brayan

Ter Abr 19, 2011 12:57
Álgebra Elementar
-
- Questão FUVEST
por LuRodrigues » Seg Abr 23, 2012 13:26
- 1 Respostas
- 1217 Exibições
- Última mensagem por Fabiano Vieira

Seg Abr 23, 2012 19:30
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![2{log}_{2}(1+\sqrt[2]{2x})-{log}_{2}(\sqrt[2]{2x})=3 2{log}_{2}(1+\sqrt[2]{2x})-{log}_{2}(\sqrt[2]{2x})=3](/latexrender/pictures/f0626009da5a28929dc47587076ba7b8.png) .Então,
.Então,  é igual a:
é igual a:
![2{log}_{2}(1+\sqrt[2]{2x})-{log}_{2}(\sqrt[2]{2x})=3 2{log}_{2}(1+\sqrt[2]{2x})-{log}_{2}(\sqrt[2]{2x})=3](/latexrender/pictures/f0626009da5a28929dc47587076ba7b8.png) .Então,
.Então,  é igual a:
é igual a:
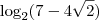 , que dá aproximadamente 0,425...
, que dá aproximadamente 0,425...



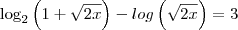
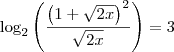


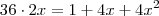

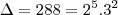 , nos dando uma raíz
, nos dando uma raíz  ...
...



![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.