





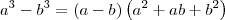 .
.![\left(\sqrt[3]{(1+2x)^2} + \sqrt[3]{1+2x} + 1\right) \left(\sqrt[3]{(1+2x)^2} + \sqrt[3]{1+2x} + 1\right)](/latexrender/pictures/cb9eb920bd3670ba578c6687ce945114.png)
![\left(\sqrt[3]{1+2x} - 1\right)\left(\sqrt[3]{(1+2x)^2} + \sqrt[3]{1+2x} + 1\right) = \left(\sqrt[3]{1+2x}\right)^3 - 1^3 = 2x \left(\sqrt[3]{1+2x} - 1\right)\left(\sqrt[3]{(1+2x)^2} + \sqrt[3]{1+2x} + 1\right) = \left(\sqrt[3]{1+2x}\right)^3 - 1^3 = 2x](/latexrender/pictures/c324c789d78b250ff0d24d1f9ec8a0ea.png)
![u = \sqrt[3]{1+2x} u = \sqrt[3]{1+2x}](/latexrender/pictures/51ffb485cdd9b52340a997c98f6ae231.png) . Teremos que quando x tende para 0, u tenderá para 1. Além disso, temos que
. Teremos que quando x tende para 0, u tenderá para 1. Além disso, temos que  . Desse modo, o limite original é equivalente a:
. Desse modo, o limite original é equivalente a: .
.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)