Pedir pra mandar a resolução é feio... aparenta preguiça... rs
Aqui costumamos pedir ajuda e receber... mas, o objetivo do fórum é aprender as propriedades necessárias para conseguir resolver o problema...
Neste caso, observe o seguinte... dois eventos (passagem de ônibus), ocorrem simultaneamente a um determinado horário (7h10) e se repetem, depois disso, em intervalos distintos (25 e 40min)...
Lembrando o conceito de multiplicação, podemos dizer que é o somatório de um mesmo número que se repete um certo tanto de vezes...
Ou seja, se o ônibus passa a cada 25 minutos, digamos que ele passe pela primeira vez num momento zero, cada horário que ele passar depois disso será múltiplo de 25... 0min, 25min, 50min, 75min... podemos, é claro converter esse tempo em horas, mas não é necessario, neste caso...
Assim, da mesma forma, o ônibus que passa a cada 40 minutos, passará em tempos que serão múltiplos de 40...
E ambos passarão ao mesmo tempo em momentos que serão tanto múltiplo de 25 quanto de 40, ou seja, em múltiplos comuns...
Partindo de um momento zero, onde ambos passam simultaneamente, como às 7h10, no exercicio, a primeira vez que isso se repetirá novamente será o menor múltiplo que 25 e 40 têm em comum, ou seja, o Mínimo Múltiplo Comum (MMC)... rs
Conhecendo o MMC, basta saber quantas vezes esse valor cabe no intervalo desejado, das 7h à meia noite...
Entretanto, como a primeira vez em que ocorrem juntos é às 7h10, podemos (ou melhor, devemos) usar esse horário como ponto zero... assim, sendo

o intervalo entre o começo e o final do experimento:
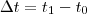
Onde

representa o tempo final (meia noite) e

o tempo inicial (7h10)
Converta o resultado em minutos e divida pelo MMC, em minutos, dos intervalos de passagem dos dois ônibus...
Assim, você encontrará a resposta deste desafio... rs
Um abraço


 o intervalo entre o começo e o final do experimento:
o intervalo entre o começo e o final do experimento: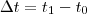
 representa o tempo final (meia noite) e
representa o tempo final (meia noite) e  o tempo inicial (7h10)
o tempo inicial (7h10)


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.