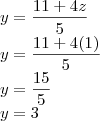Existem diversas formas. Pode ser feito por matriz, por substituição, enfim...
Por matriz é mais fácil... por substituição é melhor de entender (a meu ver)
Considerando que x, y e z mantém o mesmo valor nas três equações, o que é necessário para caracterizar o sistema de equações, pegue uma equação, encontre a relação entre uma das variáveis e as demais...
Depois, pegue outra sentença e substitua a variável que voce encontrou... assim, restarão duas variáveis... isole uma delas e siga substituindo... rs em breve voce terá o valor de uma delas e poderá, sempre substituindo, encontrar o valor das três...
Como disse, este não é o caminho mais fácil, mas permite que voce visualize bem a relação entre as variáveis...
Outro método é o da soma... da mesma forma que num sistema com duas variáveis...
Voce separa duas equações e multiplica os dois lados da igualdade de uma delas por um valor que faça com que uma das variáveis da primeira sentença se torne simétrica à da segunda equação.... então você soma os termos restantes do produto e no final te sobrarão duas variáveis numa nova equação. Voce isola uma delas e segue substituindo... rs
Pra ficar mais fácil de entender, vamos usar um outros sistema similar:

Pela soma, separamos as duas primeiras e multiplicando a primeira por -1
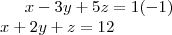
Somando as duas equações:

Podemos, então, subsitituir o y por

em qualquer das equações iniciais

Temos agora duas variáveis que podem ser substituídas por z...

Assim:
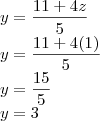
e

Certo? Existem diversos caminhos, mas idéia é sempre levar em consideração as propriedades da igualdade.
O caminho da matriz é com certeza o mais rápido, pois a matriz é um algoritmo válido para realizar esse tipo de procedimento... infelizmente, a menos que voce entenda a natureza da matriz, a solução pode parecer ter vindo por mágica, e voce acaba não entendendo o funcionamento da resolução... pela soma e pela substituição, voce visualiza o desenrolar da resolução de forma mais descritiva, ficando mais fácil aprender e não esquecer mais...
Espero ter ajudado, qualquer dúvida, é só falar....




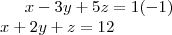

 em qualquer das equações iniciais
em qualquer das equações iniciais