 por joaofonseca » Qua Mai 04, 2011 20:50
por joaofonseca » Qua Mai 04, 2011 20:50
Seja o seguinte limite:

Ao definir o dominio da função, fiquei a saber que excluí o número 4, pois é o valor que anula o denominador. Pelo metodo experimental, fui substituindo
x por valores cada vez maiores. Cheguei à conclusão que o limite seria

. Será verdade?
Como posso chegar à mesma conclusão de uma forma analitica/algébrica?
Obrigado
Editado pela última vez por
joaofonseca em Qua Mai 04, 2011 21:10, em um total de 2 vezes.
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Qua Mai 04, 2011 21:03
por LuizAquino » Qua Mai 04, 2011 21:03
Note que:
 Sugestão
SugestãoEu acredito que o tópico abaixo possa lhe interessar.
Curso de Cálculo I no YouTubeviewtopic.php?f=137&t=4280
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por joaofonseca » Qua Mai 04, 2011 21:39
por joaofonseca » Qua Mai 04, 2011 21:39
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Qua Mai 04, 2011 23:53
por LuizAquino » Qua Mai 04, 2011 23:53
Eu recomendo que você assista a vídeo-aula "06. Cálculo I - Limites no Infinito" no meu canal no YouTube, cujo o endereço está no tópico que sugeri anteriormente.
Note que

e

. Além disso, analisando a função
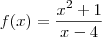
percebemos que para x > 4 temos que f(x) > 0. Considerando essas informações, temos que
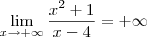
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- limite indeterminado de função racional
por jmcustodio » Sáb Set 22, 2012 22:41
- 1 Respostas
- 999 Exibições
- Última mensagem por MarceloFantini

Sáb Set 22, 2012 23:47
Cálculo: Limites, Derivadas e Integrais
-
- limite indeterminado de função racional com duas raizes
por jmcustodio » Dom Set 23, 2012 12:59
- 1 Respostas
- 1752 Exibições
- Última mensagem por MarceloFantini

Dom Set 23, 2012 13:36
Cálculo: Limites, Derivadas e Integrais
-
- Contradominio de função racional
por joaofonseca » Dom Jul 03, 2011 11:54
- 9 Respostas
- 33334 Exibições
- Última mensagem por LuizAquino

Sex Fev 10, 2012 10:52
Funções
-
- Integral de função racional
por renan_a » Qua Jan 09, 2013 17:57
- 2 Respostas
- 1972 Exibições
- Última mensagem por renan_a

Qua Jan 09, 2013 22:05
Cálculo: Limites, Derivadas e Integrais
-
- Função Racional! Ajuda urgente
por renatofbc » Qua Jun 22, 2011 22:33
- 2 Respostas
- 2233 Exibições
- Última mensagem por MarceloFantini

Qua Jun 22, 2011 23:35
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

 . Será verdade?
. Será verdade?






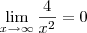
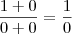
 e
e  . Além disso, analisando a função
. Além disso, analisando a função 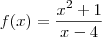 percebemos que para x > 4 temos que f(x) > 0. Considerando essas informações, temos que
percebemos que para x > 4 temos que f(x) > 0. Considerando essas informações, temos que 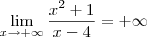
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.