 por DanielRJ » Ter Mai 03, 2011 21:17
por DanielRJ » Ter Mai 03, 2011 21:17
123-(Marck) Na igualdade:
![log_{3}{[det(2.A^{-1})]}=log_{27}{[det(2.A)^{-1}]} log_{3}{[det(2.A^{-1})]}=log_{27}{[det(2.A)^{-1}]}](/latexrender/pictures/118cf4a90adaf28c2b0bd123029488a1.png)
A é uma matriz quadrada de quinta ordem com determinante não nulo.Então det A vale:
a)

b)
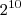
c)

d)

Quem puder pelo menos puxar o raciocinio agradeço..

-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por FilipeCaceres » Ter Mai 03, 2011 21:59
por FilipeCaceres » Ter Mai 03, 2011 21:59
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Determinantes Nivel fácil
por DanielRJ » Ter Mai 03, 2011 21:23
- 7 Respostas
- 3768 Exibições
- Última mensagem por DanielRJ

Qui Mai 05, 2011 22:17
Matrizes e Determinantes
-
- OBM - Nível 1
 por Molina » Qui Jun 11, 2009 21:38
por Molina » Qui Jun 11, 2009 21:38
- 3 Respostas
- 2875 Exibições
- Última mensagem por Molina

Dom Jun 14, 2009 14:38
Desafios Fáceis
-
- OBM - Nível 2
 por Molina » Qui Jun 11, 2009 21:51
por Molina » Qui Jun 11, 2009 21:51
- 7 Respostas
- 4186 Exibições
- Última mensagem por Cleyson007

Seg Jun 15, 2009 10:20
Desafios Médios
-
- OBM - Nível 3
 por Molina » Qui Jun 11, 2009 22:03
por Molina » Qui Jun 11, 2009 22:03
- 12 Respostas
- 8036 Exibições
- Última mensagem por BlackFoxes

Sáb Dez 26, 2009 07:44
Desafios Difíceis
-
- Nível fácil - FCC e UPE
por ingridgusmao » Dom Jun 12, 2011 02:41
- 1 Respostas
- 7533 Exibições
- Última mensagem por nietzsche

Sex Jun 24, 2011 22:54
Conjuntos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![log_{3}{[det(2.A^{-1})]}=log_{27}{[det(2.A)^{-1}]} log_{3}{[det(2.A^{-1})]}=log_{27}{[det(2.A)^{-1}]}](/latexrender/pictures/118cf4a90adaf28c2b0bd123029488a1.png) A é uma matriz quadrada de quinta ordem com determinante não nulo.Então det A vale:
A é uma matriz quadrada de quinta ordem com determinante não nulo.Então det A vale:
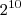




![log_{3}{[det(2.A^{-1})]}=log_{27}{[det(2.A)^{-1}]} log_{3}{[det(2.A^{-1})]}=log_{27}{[det(2.A)^{-1}]}](/latexrender/pictures/118cf4a90adaf28c2b0bd123029488a1.png) A é uma matriz quadrada de quinta ordem com determinante não nulo.Então det A vale:
A é uma matriz quadrada de quinta ordem com determinante não nulo.Então det A vale:
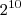




 , para matriz A de ordem n
, para matriz A de ordem n
![log_{3}{[det(2.A^{-1})]}=log_{27}{[det(2.A)^{-1}]} log_{3}{[det(2.A^{-1})]}=log_{27}{[det(2.A)^{-1}]}](/latexrender/pictures/118cf4a90adaf28c2b0bd123029488a1.png)
![det(2.A^{-1})=3^{log_{3^3}{[det(2.A)^{-1}]}}=[det(2.A)^{-1}]^{\frac{1}{3}} det(2.A^{-1})=3^{log_{3^3}{[det(2.A)^{-1}]}}=[det(2.A)^{-1}]^{\frac{1}{3}}](/latexrender/pictures/3972b641b76cdb8bf39f1f332b6caa5f.png)
![[det(2.A^{-1})]^3=[det(2.A)^{-1}] [det(2.A^{-1})]^3=[det(2.A)^{-1}]](/latexrender/pictures/fb6a7a9d24fabb4eed59e327ae891b7e.png)
![[2^5.det A^{-1}]^3=2^{-5}det A^{-1} [2^5.det A^{-1}]^3=2^{-5}det A^{-1}](/latexrender/pictures/1d1f241668ce53b348c53c0a759e215e.png)

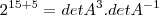
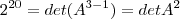
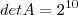



 , avisa que eu resolvo.
, avisa que eu resolvo.

