A diferença entre o número de diagonais de dois poligonos é 8. Se os dois poligonos tiverem o número de lados expresso por dois números inteiros consecutivos, a soma do número de lados dos dois poligonos é:
a) 9
b) 17
c) 19
D) 21
A fórmula é

No final da resolução eu faço uma bagunça, eu estou usando esta linha de raciocinio, não sei se esta certa:
d1-d2=8
d1=a e d2= a +1
Com esse valores eu coloco na formula. Mas no final da tudo errado, rsrs. Não chego em nenhum valor parecido.


 e
e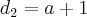 , e sim, sendo n1 e n2 o numero de lado dos poligonos:
, e sim, sendo n1 e n2 o numero de lado dos poligonos:


 e
e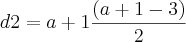
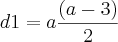



 (como d2 possu a + 1 lados e d1 possui a lados, d2 > d1)
(como d2 possu a + 1 lados e d1 possui a lados, d2 > d1)
 - >
- > 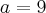


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)