 por joaofonseca » Seg Mai 02, 2011 22:56
por joaofonseca » Seg Mai 02, 2011 22:56
No meu estudo de sucessões (sequências), cheguei à parte dos limites. No plano de estudos do sistema de ensino em Portugal os limites de sucessões surgem antes dos limites de funções. Contudo, até ao momento,só encontrei bom material de apoio em relação aos limites de funções.
Sei que uma sucessão é nem mais nem menos que uma função de dominio Natural. Eu gostaria de saber se os principios que estão na base do estudo de limites de funções também se aplicam aos limites de sucessões?
Obrigado
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Seg Mai 02, 2011 23:09
por LuizAquino » Seg Mai 02, 2011 23:09
Sei que uma sucessão é nem mais nem menos que uma função de domínio Natural. Eu gostaria de saber se os princípios que estão na base do estudo de limites de funções também se aplicam aos limites de sucessões?
Basicamente sim.
Note que é válido:
Se
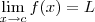
e
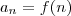
, com
c e
n naturais (sendo
n pertencente ao domínio de
f), então
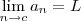
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limites]Limites com funções trigonométricas
por TuTa » Qui Jul 12, 2012 00:22
- 3 Respostas
- 2043 Exibições
- Última mensagem por e8group

Qui Jul 12, 2012 12:13
Cálculo: Limites, Derivadas e Integrais
-
- sucessões
por joanafrancisca » Ter Jul 24, 2012 23:23
- 2 Respostas
- 2264 Exibições
- Última mensagem por joanafrancisca

Qua Jul 25, 2012 01:53
Cálculo: Limites, Derivadas e Integrais
-
- sucessoes
por ulisses123 » Sex Jun 20, 2014 15:23
- 7 Respostas
- 5535 Exibições
- Última mensagem por e8group

Dom Jul 06, 2014 16:11
Sequências
-
- Limities sucessões
por matpet92 » Qui Fev 02, 2012 22:13
- 4 Respostas
- 3662 Exibições
- Última mensagem por matpet92

Dom Fev 05, 2012 20:29
Cálculo: Limites, Derivadas e Integrais
-
- Limite em sucessões - Cálculo
 por EREGON » Seg Nov 10, 2014 21:02
por EREGON » Seg Nov 10, 2014 21:02
- 6 Respostas
- 7806 Exibições
- Última mensagem por adauto martins

Qui Nov 13, 2014 14:27
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


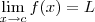 e
e 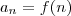 , com
, com 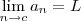 .
.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.