 por rubenesantos » Seg Mai 02, 2011 22:38
por rubenesantos » Seg Mai 02, 2011 22:38
Olá, amigos, boa noite. Sou novo no fórum e esta é minha primeira postagem.
Pois então,
Resolvendo uma lista de exercícios, me deparei com a seguinte questão:

Já resolvi outras questões desse tipo mas essa está quebrando a minha cabeça a semanas.
Eu divido o polinômio pelo outro, já que ambos tem o mesmo grau e resta a integral

Até aí eu acho que estou indo certo, mas a partir daí eu não consigo decompor esses polinômios e quando consigo sempre chego num resultado diferente do resultado da lista que é:
![x/4 - ln\left|x\right| + 1/16\left[9ln\left|2x-1\right| + 7ln\left|2x+1 \right| \right] + C x/4 - ln\left|x\right| + 1/16\left[9ln\left|2x-1\right| + 7ln\left|2x+1 \right| \right] + C](/latexrender/pictures/cbf5a3403fb012ac635cf9b826ad55c0.png)
Quem puder me ajudar, desde já agradeço!
Abraço! =D
-
rubenesantos
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Seg Mai 02, 2011 22:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Seg Mai 02, 2011 22:58
por LuizAquino » Seg Mai 02, 2011 22:58
Note que
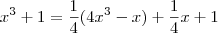
. Ou seja, temos que
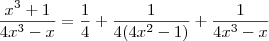
.
Portanto, você precisa resolver a integral:

Agora, aplique frações parciais na segunda e na terceira integral. Além disso, perceba que

e que

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Estou com dificuldade para resolver esta integral
por Paulo Perez » Qui Out 03, 2013 12:22
- 2 Respostas
- 4609 Exibições
- Última mensagem por Paulo Perez

Sex Out 04, 2013 16:32
Cálculo: Limites, Derivadas e Integrais
-
- Dificuldade em resolver o exercicio nº 2
por Catriane Moreira » Sáb Nov 20, 2010 23:01
- 1 Respostas
- 2166 Exibições
- Última mensagem por alexandre32100

Seg Nov 22, 2010 14:42
Matemática Financeira
-
- dificuldade em resolver matriz inversa
por oliveiracld » Qua Mar 09, 2011 00:38
- 4 Respostas
- 3849 Exibições
- Última mensagem por LuizAquino

Qua Mar 09, 2011 20:19
Matrizes e Determinantes
-
- [Funções] dificuldade para resolver
por tiaguito » Seg Out 22, 2012 17:01
- 1 Respostas
- 1831 Exibições
- Última mensagem por Russman

Seg Out 22, 2012 18:35
Funções
-
- Dificuldade para resolver esse sistema.
por 380625 » Sáb Ago 20, 2011 16:08
- 1 Respostas
- 5799 Exibições
- Última mensagem por LuizAquino

Dom Ago 28, 2011 00:32
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


![x/4 - ln\left|x\right| + 1/16\left[9ln\left|2x-1\right| + 7ln\left|2x+1 \right| \right] + C x/4 - ln\left|x\right| + 1/16\left[9ln\left|2x-1\right| + 7ln\left|2x+1 \right| \right] + C](/latexrender/pictures/cbf5a3403fb012ac635cf9b826ad55c0.png)


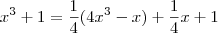 . Ou seja, temos que
. Ou seja, temos que 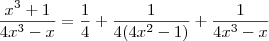 .
.
 e que
e que  .
.


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.