abel escreveu:Olá pessoal, eu sou novo aqui...
achei o fórum por acaso... preciso aprender matemática a qualquer custo xD matéria que eu sempre negligenciei na escola
tem um exercício que eu não tenho a menor idéia de como faz, não sei se alguém poderia me ajudar...
Resolva em R o sistema de inequeções

Boa noite, Abel.
O problema que você traz, trata-se de inequação matemática, ou seja, inequação nada mais é uma
"não equação". Lembra quando você estudava equação e tinha o sinal sempre de igual (=) entre as sentenças?
Por exemplo:
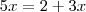
O que você deveria fazer? colocar números para um lado do sinal de igual e letras pro outro lado do sinal e resolver:

Ou seja, você chega a conclusão que

satisfaz a equação acima (basta substituir x por 1 que você vai ter certeza disso).
No caso de inequação é o mesmo pensamento. Porém, agora você trabalha com sinais diferentes do igual, ou seja, maior que.., menor que.., maior ou igual a.. e menor ou igual a..
Só tem que tomar cuidado com o sinal, pois quando você multiplica ou divide por um número negativo, inveter-se o sinal (de maior passa para menor e vice-versa).
Vou fazer o exemplo 1:

Quais os X que deixa essa setença verdadeira?
Verifique que se X < 11 a sentença é válida.
Esta é a solução.
Espero ter ajudado, bom estudo!




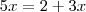

 satisfaz a equação acima (basta substituir x por 1 que você vai ter certeza disso).
satisfaz a equação acima (basta substituir x por 1 que você vai ter certeza disso).


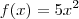 + 3x + 2 = 0
+ 3x + 2 = 0