 por LuizAquino » Seg Mai 02, 2011 09:39
por LuizAquino » Seg Mai 02, 2011 09:39
Note que
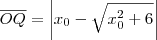
(basta tomar um x0 negativo para perceber que você deveria tomar o módulo da expressão).
Além disso, temos que

. Ou seja,

.
ObservaçãoNa grande maioria de suas mensagens aqui no fórum você não digita o texto do exercício e tão pouco a sua resolução. Você geralmente cria uma imagem desses textos e coloca aqui o endereço para ela. Por favor, eu gostaria de pedir que você parasse de fazer tal procedimento, pois ele prejudica tanto a organização do fórum quanto a utilização de ferramentas de busca. Apenas envie imagens quando for necessário.
Para a digitação das notações matemáticas esse fórum dispõe do
LaTeX. Além disso, há um
Editor de Fórmulas. Por favor, deixe a preguiça de lado e aprenda a usar esses recursos!

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por AlbertoAM » Seg Mai 02, 2011 19:06
por AlbertoAM » Seg Mai 02, 2011 19:06
Entendi porque estava ocorrendo o erro de sinal.
Vou deixar a preguiça de lado e vou começar a postar as questões com o auxílio do LaTex.Desculpe qualquer transtorno.
-
AlbertoAM
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Qui Nov 11, 2010 15:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por LuizAquino » Seg Mai 02, 2011 20:02
por LuizAquino » Seg Mai 02, 2011 20:02
Vou deixar a preguiça de lado e vou começar a postar as questões com o auxílio do LaTex. Desculpe qualquer transtorno.
Tenha certeza que aprender a usar o LaTeX será algo positivo para o seu aprendizado/participação aqui no Fórum!
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [DERIVADA] Reta tangente e Reta perpendicular
por antonelli2006 » Ter Nov 22, 2011 11:21
- 1 Respostas
- 8666 Exibições
- Última mensagem por LuizAquino

Ter Nov 22, 2011 14:28
Cálculo: Limites, Derivadas e Integrais
-
- [Reta Paralela à Reta Tangente]
por raimundoocjr » Qui Mai 30, 2013 18:44
- 0 Respostas
- 1150 Exibições
- Última mensagem por raimundoocjr

Qui Mai 30, 2013 18:44
Cálculo: Limites, Derivadas e Integrais
-
- Reta tangente
por AlbertoAM » Sáb Abr 30, 2011 15:32
- 1 Respostas
- 1524 Exibições
- Última mensagem por FilipeCaceres

Sáb Abr 30, 2011 19:13
Cálculo: Limites, Derivadas e Integrais
-
- Reta tangente
por alzenir agapito » Ter Mai 17, 2011 22:55
- 2 Respostas
- 1673 Exibições
- Última mensagem por Maykids

Qui Mai 19, 2011 12:36
Cálculo: Limites, Derivadas e Integrais
-
- Reta Tangente
por marinalcd » Sáb Out 13, 2012 16:40
- 6 Respostas
- 2406 Exibições
- Última mensagem por marinalcd

Ter Out 16, 2012 18:43
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


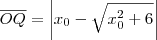 (basta tomar um x0 negativo para perceber que você deveria tomar o módulo da expressão).
(basta tomar um x0 negativo para perceber que você deveria tomar o módulo da expressão). . Ou seja,
. Ou seja,  .
.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.