Primeiro, vamos organizar o que você escreveu.
O texto "lim x-->1 t³ + t² - 5 t + 3 / t³ - 3t +2" em uma notação adequação ficaria como:
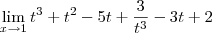
Entretanto, ao que parece você deseja mesmo calcular o limite:

Vou considerar que você quis dizer "t --> 1" quando escreveu "x --> 1".
Nesse caso, note que para
t=1 tanto o numerador quanto o denominador são 0. Isso significa que (
t-1) divide exatamente tanto o numerador quanto o denominador.
Sendo assim, você deve procurar escrever
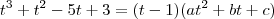
e

. Todo o seu trabalho será determinar as constantes
a,
b,
c,
d,
e e
f. Para isso, use divisão de polinômios.
SugestãoEu acredito que o tópico abaixo possa lhe interessar:
Curso de Cálculo I no YouTubeviewtopic.php?f=137&t=4280


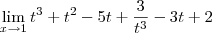

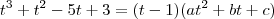 e
e  . Todo o seu trabalho será determinar as constantes a, b, c, d, e e f. Para isso, use divisão de polinômios.
. Todo o seu trabalho será determinar as constantes a, b, c, d, e e f. Para isso, use divisão de polinômios.


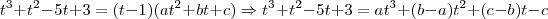

 .
.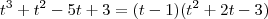 .
.

 .
.
 :
: