Teorema Raizes Racionais

por **joaofonseca** » Sáb Abr 30, 2011 13:01

Seja a seguinte função polinomial:
12x^5+6x^3-2x-8

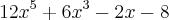
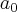Sabemos que pelo teorema das raizes racionais existe um número racional $\frac{p}{q}$ irredutivel. Sabemos também que p pode ser um dos fatores de ${a}_{0}$ e q pode ser um dos fatores de ${a}_{n}$ .
Assim ficamos com uma lista das possíveis raízes racionais deste polinomio:

$\pm1,\pm\frac{1}{2},\pm\frac{1}{3},\pm\frac{1}{4},\pm\frac{1}{6},\pm\frac{1}{12},\pm2,\pm\frac{2}{3},\pm4,\pm\frac{4}{3},\pm8,\pm\frac{8}{3}$

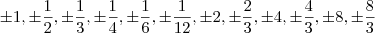
Graficamente a função tem raiz real em 0,866. Ora nenhuma destas frações resulta em 0,866. Posso então concluir que a(s) raizes desta função não são racionais!

Existe alguma técnica algébrica de decompor este polinomio de grau 5?

por **FilipeCaceres** » Sáb Abr 30, 2011 13:20

Seja a seguinte função polinomial:

Poste o enunciado completo.
Você deseja apenas fatorar essa função?

Abraço.

por **joaofonseca** » Sáb Abr 30, 2011 13:48

O enunciado é:
"Encontre os possíveis zeros utilizando o Teorema das Raizes Racionais."

Como eu não encontrei nenhum utilizando este teorema, deduzi que os zeros ou são irracionais ou imaginários. Pensei que decompondo este polinomio em polinomios de 2º grau, seria facíl encontrar os zeros, mesmo que imaginários. A minha dificuldade está mesmo em decompor o polinomio (grau 5).

A ajuda que eu estou pedindo é na decomposição do polinomio, de forma a encontrar as raizes, sejam irracionais ou imaginárias.

Obrigado

Teorema Raizes Racionais

Teorema Raizes Racionais

Teorema Raizes Racionais

Re: Teorema Raizes Racionais

Re: Teorema Raizes Racionais

Quem está online