 por alzenir agapito » Sex Abr 29, 2011 21:56
por alzenir agapito » Sex Abr 29, 2011 21:56
Ola, gostaria de saber como se calcula a derivada de
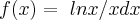
pela derivação por partes, pois, não consigo obter o resultado, por este método.
Agapito
-
alzenir agapito
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Seg Abr 25, 2011 22:27
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: matematica
- Andamento: formado
 por LuizAquino » Sex Abr 29, 2011 22:07
por LuizAquino » Sex Abr 29, 2011 22:07
"Derivada por partes"? Usualmente, o que temos é "Integral por partes". Além disso, esse diferencial "dx" na expressão de sua função não está fazendo sentido.
De qualquer modo, para derivar uma função do tipo

, use a regra do quociente:
![\left[\frac{f(x)}{g(x)}\right]^{'} = \frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2} \left[\frac{f(x)}{g(x)}\right]^{'} = \frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2}](/latexrender/pictures/c649e80828b8f7e15fc43ea811a8acc1.png)
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por alzenir agapito » Sex Abr 29, 2011 22:24
por alzenir agapito » Sex Abr 29, 2011 22:24
Sim Luiz, pela regra do quociente, eu consigo achar a resposta correta,porèm, quando aplico derivação por partes não, consigo, gostaria de visualisar qual é o meu erro.
-
alzenir agapito
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Seg Abr 25, 2011 22:27
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: matematica
- Andamento: formado
 por alzenir agapito » Sex Abr 29, 2011 22:27
por alzenir agapito » Sex Abr 29, 2011 22:27
Perdão Luiz, o caso é de integração mesmo!!!!!!!!!!!
-
alzenir agapito
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Seg Abr 25, 2011 22:27
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: matematica
- Andamento: formado
 por alzenir agapito » Sex Abr 29, 2011 22:34
por alzenir agapito » Sex Abr 29, 2011 22:34
Gostaria de ver passo a passo com a fórmula

-
alzenir agapito
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Seg Abr 25, 2011 22:27
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: matematica
- Andamento: formado
 por LuizAquino » Sex Abr 29, 2011 22:38
por LuizAquino » Sex Abr 29, 2011 22:38
Sendo assim, ao que parece você quer resolver por partes a seguinte integral:
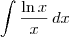
Fazendo

, temos que
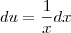
.
Fazendo
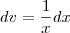
, temos que
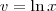
.
Usando a regra de integração por partes, temos que:
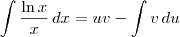
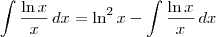
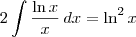
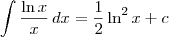
, com
c uma constante real qualquer.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por FilipeCaceres » Sex Abr 29, 2011 22:51
por FilipeCaceres » Sex Abr 29, 2011 22:51
Existe um programa muito bom onde se mostra as etapas da solução, veja como ficaria da sua questão.
http://www.wolframalpha.com/input/?i=integral%28log[e%2Cx]%2Fx%29
É só clicar em Show Step.
PS.:Você vai precisar copiar e colar o endereço.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por alzenir agapito » Sáb Abr 30, 2011 06:12
por alzenir agapito » Sáb Abr 30, 2011 06:12
Valeu Luiz
O que eu não estava visualizando é que a segunda expressão era negativa, no segundo membro e igual a expressão positiva no primeiro membro.o que daria o dobro da expressão no primeiro membro e consequentemente dividiria por 2 o segundo.
vleu mesmo!!!!!!!!!!!!!
-
alzenir agapito
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Seg Abr 25, 2011 22:27
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: matematica
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivação - derivação logarítmica
por teer4 » Ter Mai 21, 2013 12:11
- 0 Respostas
- 2157 Exibições
- Última mensagem por teer4

Ter Mai 21, 2013 12:11
Cálculo: Limites, Derivadas e Integrais
-
- parte-todo
por leticiapires52 » Sex Ago 15, 2014 13:23
- 0 Respostas
- 1668 Exibições
- Última mensagem por leticiapires52

Sex Ago 15, 2014 13:23
Números Complexos
-
- [Integral] Integração por parte...
por Jessica Seno » Dom Out 14, 2012 14:37
- 3 Respostas
- 2007 Exibições
- Última mensagem por DanielFerreira

Dom Out 28, 2012 17:17
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integração por parte
por LAZAROTTI » Ter Out 23, 2012 10:33
- 1 Respostas
- 1251 Exibições
- Última mensagem por MarceloFantini

Ter Out 23, 2012 12:03
Cálculo: Limites, Derivadas e Integrais
-
- parte da equação diferencial em f(x) e o grafico
por Bio Molina » Sáb Jun 13, 2009 18:37
- 0 Respostas
- 1044 Exibições
- Última mensagem por Bio Molina

Sáb Jun 13, 2009 18:37
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
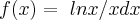 pela derivação por partes, pois, não consigo obter o resultado, por este método.
pela derivação por partes, pois, não consigo obter o resultado, por este método.
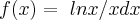 pela derivação por partes, pois, não consigo obter o resultado, por este método.
pela derivação por partes, pois, não consigo obter o resultado, por este método.
 , use a regra do quociente:
, use a regra do quociente:![\left[\frac{f(x)}{g(x)}\right]^{'} = \frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2} \left[\frac{f(x)}{g(x)}\right]^{'} = \frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2}](/latexrender/pictures/c649e80828b8f7e15fc43ea811a8acc1.png)





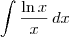
 , temos que
, temos que 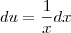 .
.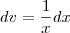 , temos que
, temos que 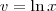 .
.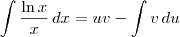
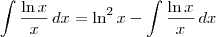
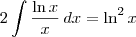
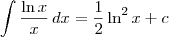 , com c uma constante real qualquer.
, com c uma constante real qualquer.


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.