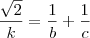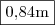por Alexander » Qui Abr 28, 2011 21:48
por Alexander » Qui Abr 28, 2011 21:48
(EAM) Para sustentação do letreiro é feito suporte de ferro na forma de um triângulo retângulo ABC. Calcule o comprimento da barra de ferro representada pelo segmento AD, sabendo que é bissetriz do ângulo BÂC.
A:0,56m B:0,84m C:0,92m D:1m E:1,2m
Eu usei o teorema de Pitágoras e encontrei
![80\sqrt[]{7} 80\sqrt[]{7}](/latexrender/pictures/04f438abfaf2c9fcb1e2eba10bd9c006.png)
. Depois usei relações métricas no triângulo retângulo pra achar a "altura", deu
![30\sqrt[]{7} 30\sqrt[]{7}](/latexrender/pictures/8b6a1c193e462d9267e6005aff8ede8d.png)
. Não cola com o resultado.
Ajude-me!
- Anexos
-

- Imagem do triângulo.
- EAM-imagem.jpg (41.09 KiB) Exibido 6963 vezes
"Se não puder se destacar pelo talento, vença pelo esforço." - Dave Weinbaum
-
Alexander
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qua Nov 24, 2010 23:10
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por FilipeCaceres » Sex Abr 29, 2011 00:37
por FilipeCaceres » Sex Abr 29, 2011 00:37
Observe que o enunciado diz que a reta AD é a bissetriz do triângulo,portanto o que você precisa calcular é o valor da sua bissetriz.
Vou deixar para você pesquisar e mostrar que,

Onde,
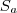
é a medida da bissetriz

os lados do triângulo

o perímetro do triângulo
Dica: Use a relação de Stewart para encontrar a fórmula.
Tente resolver agora, caso não consiga poste o que você conseguiu fazer que lhe ajudaremos com o resto.
Uma outra coisa, o que são esses teus valores A:0,56m B:0,84m C:0,92m D:1m E:1,2m ?
Abraço.
Editado pela última vez por
FilipeCaceres em Sex Abr 29, 2011 00:56, em um total de 1 vez.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Fabricio dalla » Sex Abr 29, 2011 00:48
por Fabricio dalla » Sex Abr 29, 2011 00:48
nunca vi essa formula de relação de Stewart!!
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por FilipeCaceres » Sex Abr 29, 2011 01:09
por FilipeCaceres » Sex Abr 29, 2011 01:09
- stewart.PNG (8.4 KiB) Exibido 6946 vezes
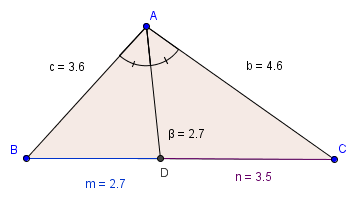
Para um triângulo ABC, no caso de tomarmos a bissetriz

do ângulo
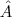
dividindo o lado

em dois segmentos

e
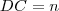
, a relação de Stewart pode ser escrita assim:

e, sendo também verdade que


Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por FilipeCaceres » Sex Abr 29, 2011 01:38
por FilipeCaceres » Sex Abr 29, 2011 01:38
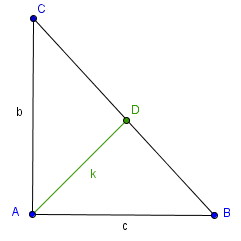
- relacao_metrica.PNG (5.18 KiB) Exibido 6944 vezes
Seja ABC um triângulo retângulo em que b=AC, c=AB; D é o pé da bissetriz do ângulo em A; k=AD.
Verifica-se que
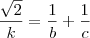
E neste caso a resposta sai direto, mas sempre devemos mostrar da onde sai esta relações.
Por se tratar de um triângulo retângulo devemos ter em mente as principais relações métricas, veja
viewtopic.php?f=117&t=4388&p=14509Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Alexander » Sex Abr 29, 2011 10:31
por Alexander » Sex Abr 29, 2011 10:31
FilipeCaceres escreveu:Uma outra coisa, o que são esses teus valores A:0,56m B:0,84m C:0,92m D:1m E:1,2m ?
São as opções. Isso é uma questão da Escola de Aprendiz-marinheiro (EAM).
Ok. Já estou pesquisando. Agora, uma coisinha: Isso está em livro de ensino fundamental, né? Porque a prova é de nível fundamental.
Eu estudei os livros do Álvaro Andrini, Praticando matemática (todos) e não estou lembrando dessa Relação de Stewart. O que eu estudei foi relações métricas no triângulo retângulo.
Mas, não tem problema. Estou pesquisando nos livros do Dante. Vou tentar entender a questão com as dicas.
"Se não puder se destacar pelo talento, vença pelo esforço." - Dave Weinbaum
-
Alexander
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qua Nov 24, 2010 23:10
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por FilipeCaceres » Sex Abr 29, 2011 10:42
por FilipeCaceres » Sex Abr 29, 2011 10:42
Só para lhe ajudar,
A resposta é
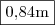
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Triângulo retângulo] Bissetriz interna
por Ricardo MB » Seg Jul 21, 2014 22:44
- 0 Respostas
- 2053 Exibições
- Última mensagem por Ricardo MB

Seg Jul 21, 2014 22:44
Geometria Plana
-
- [Geometria Plana - Triângulo] Triângulo Isós. e Bissetriz
por raimundoocjr » Qua Fev 22, 2012 09:41
- 3 Respostas
- 6601 Exibições
- Última mensagem por DanielFerreira

Sáb Fev 25, 2012 01:37
Geometria Plana
-
- Calculos envolvendo triângulo retângulo e retângulo
 por andersontricordiano » Seg Abr 18, 2011 02:29
por andersontricordiano » Seg Abr 18, 2011 02:29
- 1 Respostas
- 4034 Exibições
- Última mensagem por MarceloFantini

Seg Abr 18, 2011 04:19
Progressões
-
- [Geometria Plana - Triângulo] Altura e Bissetriz
por raimundoocjr » Ter Fev 21, 2012 09:39
- 2 Respostas
- 2997 Exibições
- Última mensagem por Arkanus Darondra

Ter Fev 21, 2012 12:54
Geometria Plana
-
- Triangulo Retangulo
por ginrj » Qui Jun 04, 2009 18:56
- 1 Respostas
- 3409 Exibições
- Última mensagem por ginrj

Seg Jun 15, 2009 18:14
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![80\sqrt[]{7} 80\sqrt[]{7}](/latexrender/pictures/04f438abfaf2c9fcb1e2eba10bd9c006.png) . Depois usei relações métricas no triângulo retângulo pra achar a "altura", deu
. Depois usei relações métricas no triângulo retângulo pra achar a "altura", deu ![30\sqrt[]{7} 30\sqrt[]{7}](/latexrender/pictures/8b6a1c193e462d9267e6005aff8ede8d.png) . Não cola com o resultado.
. Não cola com o resultado.
![80\sqrt[]{7} 80\sqrt[]{7}](/latexrender/pictures/04f438abfaf2c9fcb1e2eba10bd9c006.png) . Depois usei relações métricas no triângulo retângulo pra achar a "altura", deu
. Depois usei relações métricas no triângulo retângulo pra achar a "altura", deu ![30\sqrt[]{7} 30\sqrt[]{7}](/latexrender/pictures/8b6a1c193e462d9267e6005aff8ede8d.png) . Não cola com o resultado.
. Não cola com o resultado.

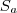 é a medida da bissetriz
é a medida da bissetriz os lados do triângulo
os lados do triângulo o perímetro do triângulo
o perímetro do triângulo

 do ângulo
do ângulo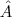 dividindo o lado
dividindo o lado  em dois segmentos
em dois segmentos  e
e 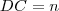 , a relação de Stewart pode ser escrita assim:
, a relação de Stewart pode ser escrita assim: